Разложим число 19600 на простые множители:
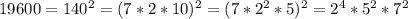
Делителем этого числа будет некое число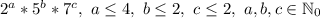 
.
Не забудем также, что в разложение числа можно добавить единицу в любой степени (обозначим показатель степени единицы за x).
а) Может ли эта прогрессия состоять из 3 членов?
Пусть такая прогрессия существует. Тогда произведение её членов равно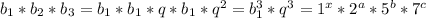 
.
Мы видим, что возможно найти кубы чисел в данном разложении: например, можно взять куб единицы и куб двойки. Приведём пример: пусть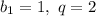 
. Тогда произведение членов этой прогрессии равно 
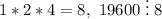. Такое может быть.
б) Может ли эта прогрессия состоять из 5 членов?
Пусть такая прогрессия существует. Тогда произведение её членов равно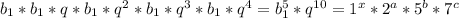 
.
Если самую большую степень отдать под единицу, то есть 10, то остаётся пятая степень, а в разложении максимально возможная степень — это 4. Если бы мы отдали пятую степень под единицу, тем более случай бы не реализовался.
Случай с ненатуральным знаменателем прогрессии также не реализуется, так как первый её член — это как минимум четвёртая степень какого-то числа, которое стоит в знаменателе q (если q — рациональное число). При перемножении всех пяти членов в произведении будет как минимум двадцатая степень, которой нет в разложении (единица не в счёт, иначе знаменатель будет натуральным числом). Иррациональным знаменатель прогрессии быть не может, иначе некоторые его члены будут также иррациональны.
Таким образом, прогрессия не может состоять из 5 членов.
в) Может ли эта прогрессия состоять из 4 членов?
Пусть такая прогрессия существует. Тогда произведение её членов равно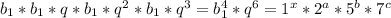 
.
Шестую степень можно отдать под единицу, а четвёртую – под двойку. Тогда мы получим такую прогрессию: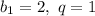 
. Произведение её членов равно 
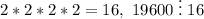. То есть такое может быть.
ответ: а) да; б) нет; в) да
наименьшее двузначное, кратное 5: 10 наибольшее трехзначное, кратное 3: 999. 10+999+х. 1009+х. Число коатно 4-ем, если две последние цифры составляют число, кратное 4. Ближайшее к 9-ти- это 12. Значит, х+9=12 х=12-9=3 ответ:3