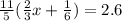
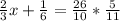
Любой многочлен степени n вида представляется произведением постоянного множителя при старшей степени и n линейных множителей , i=1, 2, …, n, то есть , причем , i=1, 2, …, n являются корнями многочлена.
Эта теорема сформулирована для комплексных корней , i=1, 2, …, n и комплексных коэффициентов , k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители.
Если коэффициенты , k=0, 1, 2, …, n – действительные числа, то комплексные корни многочлена ОБЯЗАТЕЛЬНО будут встречаться комплексно сопряженными парами.
К примеру, если корни и многочлена являются комплексно сопряженными, а остальные корни действительные, то многочлен представится в виде , где
ответ:
пошаговое объяснение:
объем любого прямоугольного параллелепипеда равен произведению длины, ширины и высоты этого прямоугольного параллелепипеда.
согласно условию , длина данного прямоугольного параллелепипеда равна 8 метров, его ширина составляет 9 метров, а высота этого параллелепипеда равна 12 метрам, следовательно, объем v данного прямоугольного параллелепипеда составляет:
v = 8 * 9 * 12 = 72 * 12 = 864 м³.