Саму задачу можно переформулировать немного по-другому:
Было: Расставить минимальное количество шашек на шахматной доске 8 на 8, так чтобы было невозможно поставить коня так, чтобы он не бил ни одной шашки.Переходит в: расставить на доске минимальное количество коней так, чтобы было невозможно поставить шашку не под удар коня.Если мы решим вторую задачу, то просто нужно будет заменить коней шашками - и мы получим искомое расположение.
По поводу второй задачи можно заметить, что:
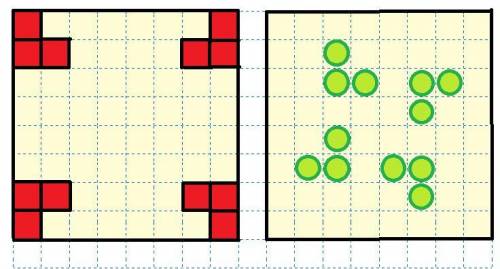
Разные кони должны бить выделенные красным клетки на рисунке ниже.Отсюда следует, что мы не можем расставить менее, чем 4 * 3 = 12 коней. Если это можно сделать, то задача решится. И да, это получилось сделать (рисунок 2).
Заменяем коней шашками и получаем ответ: 12 коней.
ответ: 12 шашек.
Пошаговое объяснение:
1) 4+(7/4)*√(5¹¹/₄₉)=4-5*√(256/49)=4-(7/4)*(16/7)=4-7*16/(4*7)=4-4=0.
2)
14x²-5x-1=0 D=5²-4*14*(-1)=25+56=81. √D=9.
x₁=(5+9)/(2*14)=14/28=1/2.
x₂=(5-9)(2*14)=-4/28=-1/7.
ответ: x₁=1/2 x₂=-1/7.
3)
5/(x-2)+1=14/(x²-4x+4)
5/(x-2)+1=14/(x-2)²
Пусть x-2=t ⇒
(5/t)+1=14/t² |×t²
5t+t²=14
t²+5t-14=0 D=81 √D=9
t₁=x-2=2 x₁=4
t₂=x-2=-7 x₂=-5.
ответ: x₁=4 x₂=-5.
4)
9x⁴-40x²+16=0
Пусть x²=t≥0
9t²-40t+16=0 D=1024 √D=32
t₁=x²=4 x=√4 x₁=2 x₂=-2
t₂=x²=4/9 x=√(4/9) x₃=2/3 x₄=-2/3.
ответ: x₁=2 x₂=-2 x₃=2/3 x₄=-2/3.
5)
x*(x²-16)/(x²-9)≤0
x*(x²-4²)/(x²-3²)≤0
x*(x+4)*(x-4)/(x+3)*(x-3)≤0 ОДЗ: x+3≠0 x≠-3 x-3≠0 x≠3.
-∞__-__-4__+__-3__-__0__+__3__-__4__+__+∞
ответ: x∈(-∞;-4]U(-3;0]U(3;4].
6)
(6-x)/(x²+2x+5)≥0
(6-x)/(x²+2x+1+4)≥0
(6-x)/((x+1)²+4)≥0
Так как ((х+1)²+4)>0 ⇒
6-x≥0
x≤6.
ответ: x∈(-∞;6].
0,3
0,02
1
0,05
0,035
250
3
0,06
0,002
0,4
0,25
2
0,09
10
0,07
35
0,03
0,1
50
0,2
15
4
0,01
0,08