Необходимым условием для существования решение является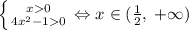 
; Теперь можно преобразовать: 
;
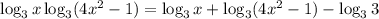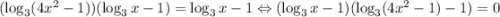; Отсюда легко найти корни: 
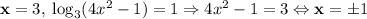; Удовлетворяют найденному в начале промежутку лишь два корня - 1 и 3.
ответ: 1; 3
Рассмотрим отрезок ![[\log_{5}2,\; \log_{5}27]](/tpl/images/1043/7471/c6c6d.png)
; Теперь отвлечемся. Пусть дан отрезок ![[a,\; b]](/tpl/images/1043/7471/62cfb.png)
; Если ![x_{0}\in[a,\;b] \Leftrightarrow 5^{x_{0}}\in[5^{a},\;5^{b}]](/tpl/images/1043/7471/3a7be.png)
; Для нашего отрезка: ![5^{x_0}\in[2,\;27]](/tpl/images/1043/7471/b2080.png)
; Очевидно, что 3 не входит (5*5*5=125), но 1 подходит.
ответ: 1.
Предположим, что х (га) - это площадь поля, тогда тракторист вспахал в первый день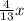
(га), следовательно, во второй день он вспахал - 
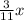(га), а в третий - 12 га
согласно этим данным составляем уравнение:
умножаем на 143 для того чтобы избавится от знаменателя
44х+39х+1716=143х
83х+1716=143х
143х-83х=1 716
60х=1 716
х=1 716:60
х=28,6 (га)
ответ: 28,6 га площадь поля.
Проверка:
(га) - вспахал тракторист в I день.
(га) – вспахал тракторист во II день.
8,8+7,8+12=28,6 (га) – площадь поля.