∠M=45°
Пошаговое объяснение:
Определим угол в вершине треугольника MPK как угол между векторами MP и MK:
MP = OP - OM = (1; 4) - (-3 ;-2) = (1-(-3); 4-(-2)) = (4; 6)
MK = OK - OM = (2; -1) - (-3 ;-2) = (2-(-3); -1-(-2)) = (5; 1).
Скалярное произведение векторов MP(x₁; y₁) и MK(x₂; y₂) можно определить по формулам:
MP·MK=x₁·x₂+y₁·y₂ и MP·MK=|MP|·|MK|·cosα,
где |MP| и |MK| длины векторов MP и MK, α=∠M - угол между векторами MP и MK.
Определяем длину векторов MP и MK:
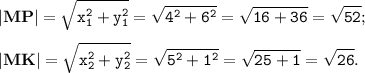
Скалярное произведение векторов MP(x₁; y₁) и MK(x₂; y₂) определяем через координаты:
MP·MK=4·5+6·1=26.
Тогда косинус угла между векторами MP и MK равен:
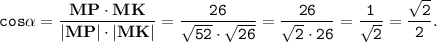
Так как
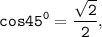
то ∠M=45°.
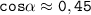
Пошаговое объяснение:
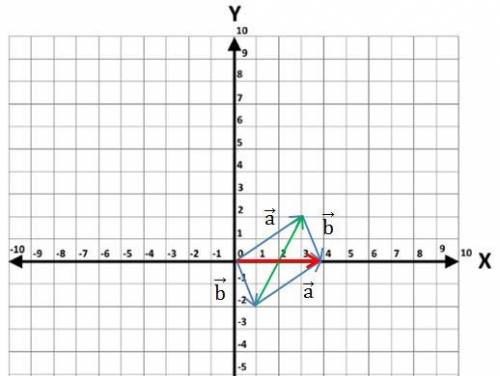
Векторы d1 и d2, направленные по диагоналям параллелограмма определяем как разность векторов a и b (см. рисунок: зелёный вектор) и как сумма векторов a и b (см. рисунок: красный вектор):
d1 = a - b = (3; 2) - (1; -2) = (3-1; 2-(-2)) = (2; 4),
d2 = a + b = (3; 2) + (1; -2) = (3+1; 2+(-2)) = (4; 0).
Скалярное произведение векторов d1(x₁; y₁) и d2(x₂; y₂) можно определить по формулам:
d1·d2=x₁·x₂+y₁·y₂ и d1·d2=|d1|·|d2|·cosα,
где |d1| и |d2| длины векторов, соответственно, d1 и d2, α - угол между векторами d1 и d2.
Определяем длины векторов d1 и d2:
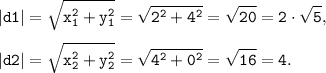
Скалярное произведение векторов d1(x₁; y₁) и d2(x₂; y₂) определяем через координаты:
d1·d2=2·4+4·0=8.
Тогда косинус угла между векторами d1 и d2 равен:
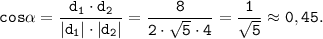
Пошаговое объяснение:
1 м³ = 1000 дм³
1 дм = 1000 см³ = 1 л
Вычисляем в кубических дециметрах.
4*1000 + 0,9 - 180 + 0,7 = 3820 + 1,6 = 3821,6 дм³ = 3 м³ 821 дм³ 600 см³