В некотором царстве, в некотором государстве жили-были проценты. Жили они дружно и в согласии, пока однажды не поспорили 50 % и 20% о том, кто из них важнее и главнее.
"Я больше, чем ты, - сказал 50%, - поэтому я важнее".
"Может ты и больше, но более жадный, чем я. Видишь на волшебной яблоньке созрели 10 яблок. Заберёшь ты свою долю, а остальным останется всего 5 яблок. Я же оставлю другим 8 яблок. Видишь, какой ты жадный!" - ответило 20%.
"Это я то жадный, - возмутился 50 %, - а если я к тем 10 яблонькам захочу прибавить свой процент, тогда ведь яблок станет 15 штук. А ты? Их станет всего лишь 12. Значит, я щедрый, а жадный ты!"
Услышал 100% их спор, подошёл к ним и сказал: " Мы все равноправны. Например, захотят два мальчика из Тридевятого царства поделить 10 конфет напополам, так им И съедят мальчики каждый по 5 конфет. А если мальчиков будет пять, то им каждому по 2 конфеты. Мы все по своему нужны и все по-своему важны!"
Подробнее - на -
Пошаговое объяснение:
Вначале заметим, что:
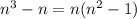
Докажем, что нечетное число в квадрате всегда дает остаток 1 при делении на 8 (поэтому, если отнять 1, то получится число, делящееся на 8):
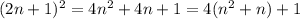
Данное число (если отнять 1) делится на 4 по разложению и еще на 2, так как n²+n по-любому четное (нечет. + нечет. = чет.). И: 4*2=8.
То есть, второй множитель, и, тогда, само число делится на 8. И нужно доказать, что оно еще должно делиться на 3.
1. Если n кратно трем, то задача решена: один множитель кратен 3, и, тогда, само произведение.
2. n не делится на 3. Докажем, что квадрат числа (если оно не делится на 3 и имеет остатки либо 1, либо 2) всегда дает остаток 1 при делении на 3 (и если от него отнять 1, то получится число, делящееся на 3):
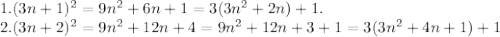
Итого: если число делится и на 3, и на 8, то оно делится на 3*8=24, что и требовалось доказать!
ответ:нормальная конечно у вас домашка...
Пошаговое объяснение: