Пусть A=2ⁿ⁺²*3ⁿ+5n-4
1) n=1: A₁=2³*3¹+5*1-4=24+1=25⋮25
2) Пусть 2ⁿ⁺²*3ⁿ+5n-4 ⋮ 25 для некоторого n=k, то есть ⋮25. Докажем, что условие верно и для n=k+1
Получаем:
⋮25=>⋮25;
25(1-k)⋮25;
Значит ⋮25.
Ч.т.д.
______________________
Доказано методом математической индукции
Пусть A=2ⁿ⁺²*3ⁿ+5n-4
1) n=1: A₁=2³*3¹+5*1-4=24+1=25⋮25
2) Пусть 2ⁿ⁺²*3ⁿ+5n-4 ⋮ 25 для некоторого n=k, то есть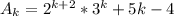 ⋮25. Докажем, что условие верно и для n=k+1
⋮25. Докажем, что условие верно и для n=k+1
Получаем: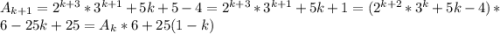
25(1-k)⋮25;
Значит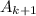 ⋮25.
⋮25.
Ч.т.д.
______________________
Доказано методом математической индукции