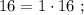
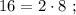
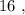т.е.: 
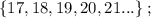
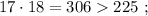
каждое – будет, очевидно, больше чем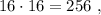 
т.е. больше 
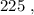а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.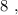
т.е.: 
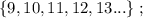
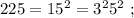
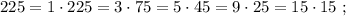
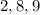и 
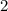и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы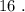 
и никаких натуральных чисел нет. и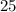 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы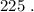 
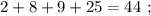
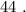
называют величину
Если это выражение возвести в квадрат и слева и справа,
то мы получим, что:
или просто:
Тогда условие задачи, можно переформулировать так: «произведение двух самых маленьких чисел равно
Произведение 16 можно составить из разных натруральных чисел
только двумя
I.
II.
Поскольку это должны быть минимальные числа,
то остальные числа могут быть только больше.
I* В первом случае остальные числа могут быть только больше
Но произведение даже
И произведение любых двух чисел, больших, чем
II* Во втором случае остальные числа могут быть только больше
Рассмотрим разложение на множители числа
На подойдут только числа, большие восьми и не равные друг другу,
т.е.
Таким образом Вася выбрал числа
В диапазон между
Между
В диапазон между
Сумма всех Васиных чисел:
О т в е т :