Покажите, что чётные числа 18, 20, 48, 96 можно записать в виде 2*k, где k- некоторое натуральное число. !

👇

Увидеть ответ

Ответ:

Pyc52141

08.08.2021

18:2 = 9, k = 9

2*9 = 18

20:2 = 10, k = 10

2*10 = 20

48:2 = 24, k = 24

2*24 = 48

96:2 = 48, k = 48

2*48 = 96

4,6(85 оценок)

Открыть все ответы

Ответ:

dariak98

08.08.2021

ответ: (2, -1, 1)

Пошаговое объяснение: Запишем систему уравнений в матричном виде.

$\left[\begin{array}{cccc}3&-1&2&9\\2&3&-1&0\\2&4&3&3\end{array}\right]$

Приведем к ступенчатому виду. Применяем операцию 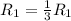$R_1=\frac{1}{3} R_1$ к R_1 (к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.

$\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]$

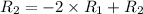Применяем операцию $R_2=-2\times R_1+R_2$ к R_2 (ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.

$\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]$

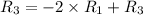Применяем операцию $R_3=-2\times R_1+R_3$ к R_3 (к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.

$\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&\frac{11}{3} &-\frac{7}{3}&-6 \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]$

Применяем операцию 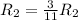$R_2=\frac{3}{11}R_2$ к R_2 для того, чтобы сделать некоторые элементы строки равными 1.

$\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&1&-\frac{7}{11} &-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]$

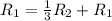Применяем операцию $R_1=\frac{1}{3} R_2+R_1$ к R_1 для того, чтобы сделать некоторые элементы равными 0.

$\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]$

Применяем операцию $R_3=-\frac{14}{3} R_2+R_3$ к R_3 для того, чтобы сделать некоторые элементы строки равными 0.

$\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&\frac{51}{11} &\frac{51}{11} \end{array}\right]$

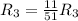Применяем операцию $R_3=\frac{11}{51} R_3$ к R_3 для того, чтобы сделать некоторые элементы строки равными 1.

$\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]$

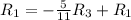Применяем операцию $R_1=-\frac{5}{11}R_3+R_1$ к R_1 для того, чтобы сделать некоторые элементы строки равными 0.

$\left[\begin{array}{cccc}1&0&0&2 \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]$

Применяем операцию 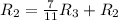$R_2=\frac{7}{11}R_3+R_2$ к R_2 для того, чтобы сделать некоторые элементы равными 0.

$\left[\begin{array}{cccc}1&0&0&2\\0&1&0&-1\\0&0&1&1\end{array}\right]$

Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.

x=2

y=-1

z=1

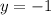
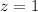
Решением является множество упорядоченных пар, которые удовлетворяют системе.

(2, -1, 1)

4,5(49 оценок)

Ответ:

andrew22091996

08.08.2021

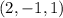
НОК(3;6) = 6

Объяснение:

разложим числа на простые множители.

сначала запишем разложение на множители самого большого число, а затем наименьшее число. подчеркнем в разложении меньшего числа множители, которые не вошли в разложение наибольшего числа

6 = 2 • 3

3 = 3

чтобы определить НОК, необходимо недостающие множители (эти множителей подчёркнуты) добавить множителя в большого числа и перемножить их:

НОК(3; 6) = 2 • 3 = 6

НОК(28; 9) = 252

Объяснение:

Разложим числа на простые множители.

Сначала запишем разложение на множители самого большого число, затем наименьшее число. Подчеркнем разложение меньшего числа множители, которые не вошли в разложение наибольшего числа.

28 = 2 • 2 • 7

9 = 3 • 3

Чтобы определить НОК, необходимо недостающие множители (эти множители подчёркнуты) добавить к множителям большого числа и перемножить их:

НОК(28; 9) = 2 • 2 • 7 • 3 • 3 = 252

НОК(15;20) = 60

Объяснение:

Разложим числа на простые множители.

Сначала запишем разложение на множители самого большого число, затем наименьшее число.

Подчеркнем в разложении меньшего числа множители, которые не вошли в разложение меньшего числа.

20 = 2 • 2 • 5

15 = 3 • 5

НОК(15; 20) = 2 • 2 • 5 • 3 = 60