Давай поровну=)
Два с десятичными дробями:
1) 0,22x = 2,42
x = 2,42/0,22
x = 242/22
x= 11
На втором примере уравнения объясню, как они составляются.
Начинаем решать задачу от обратного: у нас есть ответ, х = 11.
Выбираем действие, например, умножение (оно уже было, но для того, чтобы понять, как это делается).
Теперь умножим число 11 на какое-нибудь целое число, например 14.
11*14=154.
В принципе, все готово. Заменим теперь число 11 на х, а остальные числа поделим на 100.
x*0.14=1.54
Перепишем уравнение в более правильный вид:
Итак, 2) 0,14х=1,54.
Решив, уравнение, проверим, что х=11.
С десятичными дробями немного больше действий нужно произвести
3)
Делаем все то же самое. Идем от обратного. ответ есть, по-прежнему х=11. Так же выбираем действие, ну на этот раз можно привести сложение.
Уже получаем шаблон уравнения: 11+ дробь = дробь
Выберем любую дробь, например 7/8.
Получаем уравнение 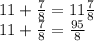
Заменим 11 на х и получим, что в этом уравнении:
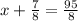 \\
\\
также получим ответ 11.
Ну и
4) 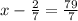
Так же x=11
х = 2у² - 4у + 3, даёт уравнение параболы, повёрнутой относительно оси Ох.
Приведение заданного уравнения к каноническому виду дано в приложении.
Для нахождения точек пересечения параболы х - 2у² + 4у - 3=0 с прямой x - 2у + 1=0 сделаем подстановку х = 2у - 1 в уравнение параболы:
2у - 1 - 2у² + 4у - 3 = 0,
2у² - 6у + 4 = 0 или, сократив на 2:
у² - 3у + 2 = 0.
Квадратное уравнение, решаем относительно y: Ищем дискриминант:
D=(-3)^2-4*1*2=9-4*2=9-8=1;Дискриминант больше 0, уравнение имеет 2 корня:
y₁=(√1-(-3))/(2*1)=(1-(-3))/2=(1+3)/2=4/2=2;y₂=(-√1-(-3))/(2*1)=(-1-(-3))/2=(-1+3)/2=2/2=1.
Находим значения х:
х₁ = 2у - 1 = 2*2 - 1 = 3,
х₂ = 2*1 - 1 = 1.