Площадь увеличилась на 44%, а периметр увеличился на 20%.
Пошаговое объяснение:
1. Пусть сторона первоначального квадрата равна х см, тогда его площадь S1 = x^2 см^2, а периметр Р1 = 4х см.
2, После увеличения на 20% сторона квадрата станет равной х + 0,2х = 1,2х см. Площадь нового квадрата S2 = (1,2x)^2 = 1,44x^2 см^2, а периметр Р2 = 4•1,2х = 4,8х см.
3. S2/S1 = 1.44x^2/x^2 = 1,44 = 144% составляет площадь нового квадрата по отношению к площадь первоначального.
144% - 100% = 44% - на столько процентов увеличилась площадь.
4. Р2/Р1 = 4,8х/4х = 1,2 = 120% составляет периметр нового квадрата по отношению к периметру первоначального.
120% - 100% = 20% - на столько процентов увеличился периметр.
0,99144
Пошаговое объяснение:
Для решения задачи воспользуемся формулой Бернулли для повторных испытаний. Пусть вероятность изделия оказаться бракованным это p=0,1. Вероятность изделия оказаться хорошим это q=0,9.
Партия будет принята без сплошного контроля, если из пяти изделий не будет вообще бракованных, либо одно бракованное, либо - два.
Найдем по очереди вероятности каждого из подходящих исходов:
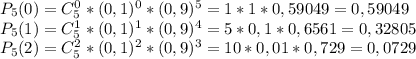
Просуммируем полученные вероятности:
0,59049+0,32805+0,0729=0,99144
Это и будет вероятность того, что партия будет принята без сплошного контроля.
Пункт В), промежуток [ -3:0].
sin^2(x) от нуля до 1
3sin^2(x) от нуля до 3
3sin^2(x)-3 от -3 до 0