вес 1-го раствора = х кг
вес 2-го раствора = у кг
вес кислоты в 1-м растворе=0,14х
вес кислоты в 2-м растворе=0,5у
полученный раствор=0,22(х+у+10)
получаем уравнение
0,14х+0,5у=0,22(х+у+10)
теперь выполняем по тому же принципу условие ЕСЛИ
0,14х+0,5у+0,5*10=0,32(х+у+10)
решить проще такую систему методом вычитания
(2-е уравнение-1-е ур-ние)
5=0,1(х+у+10)
50=х+у+10
х+у=40
у=40-х
подставляем в 1-е ур-ние
0,14х+0,5(40-х)=0,22(40+10)
0,14х+20-0,5х=11
0,36х=9
х=9/0,36=25 кг14-процентного растовра использовали для получения смеси
39 км равнина, 20 км в гору, 15 км под уклон.
Пошаговое объяснение:
Пусть длина подъёма в гору х км, тогда длина участка под уклон равна 0,75х км, а равнинный участок равен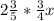 км. Длина всей велотрассы - сумма этих трёх участков, т.е.
км. Длина всей велотрассы - сумма этих трёх участков, т.е.
20 км - в гору
0.75*20 = 15 (км) - под уклон
74-20-15 = 39 (км) - равнина