Question

Решите уравнения: 1) 1 + х + х^2 + + х^99 = 0 2) х^2 - 2х^3 + 4х^4 - 8х^5 + = 2х +1, |х|< 1 3) 2х + 1 + х^2 - х^3 + х^4 - х^5 + = 13/6, |х|< 1

Answer 1

1)

Проверим точку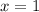 $x = 1$. Равенство не выполняется.

Значит, домножим и поделим на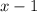 $x - 1$.

Получим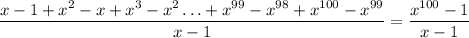 $\displaystyle {{x - 1 + x^2 - x + x^3 - x^2 \ldots + x^{99} - x^{98} + x^{100} - x^{99}} \over{x - 1}} = \displaystyle{x^{100} - 1 \over{x - 1}}$.

Имеем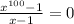 $\frac{x^{100} - 1}{x - 1} = 0$.

Выражение в числителе над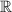 $\mathbb{R}$ эквивалентно 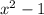$x^2 - 1$, т.к. имеет те же корни $x^{100} = 1 \Rightarrow x = \sqrt[100]{1} = \pm 1$.

Значит, единственный корень: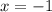 $x = -1$.

2)

При данных ограничениях решить уравнение невозможно. Сумма слева может расходиться (т.е равняться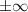 $\pm\infty$), ведь знаменатель прогрессии $-2x$.

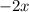Пусть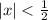 $|x| < \frac12$

Слева имеем сумму бесконечно убывающей геометрической прогрессии. Значит выражение можно свернуть в:

$\frac{x^2}{1 + 2x} = 2x + 1$

Или $x^2 = (2x + 1)^2 \Rightarrow (x + 1)(3x + 1) = 0$.

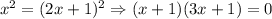По условию подходит один корень: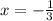 $x = -\frac{1}{3}$

3)

Для простоты преобразуем к виду:

$1 - x + x^2 - x^3 + x^4 - x^5 + \ldots = \frac{13}{6} - 3x$.

Слева сумма бесконечно убывающей геометрической прогрессии.

$\frac{1}{1 + x} = \frac{13}{6} - 3x$

$-3x^2 - \frac{5x}{6} + \frac{7}{6} = 0$.

И корни:

$x = -\frac{7}{9}\\x = \frac{1}{2}$