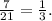Чтобы дробь достигала минимального значения, числитель должен быть минимален, а знаменатель - максимальным. Заметим, что как в числителе, так и в знаменателе квадратные уравнения относительно a и b, причем в уравнении относительно a, минимальное значение которого нас интересует, коэффициент возле x² больше нуля, следовательно, ветки параболы направлены вверх, и минимальное значение функция принимает в вершине параболы.
В уравнении относительно b ветки параболы направлены вниз, следовательно, максимальное значение достигается так же в вершине параболы.
Вычислим абсциссы вершин парабол по формуле x=, где a и b - коэффициенты перед x² и x соответственно.
Абсцисса вершины параболы для функции относительно a x=.
Значение ординаты в этой точке найдём, подставив полученное значение x в уравнение, получим:
y=9-18+16=7
Проделаем то же для уравнения в знаменателе, получим:
2) В магазине проводится акция, тому, кто купить 2 шерстяные кофты, рубашка продается за полцены. Сколько заплатит покупатель за эти вещи? 30,7*2+0,5*28,3=61,4+14,15=75,55≈75,6 3) В магазине проводится акция, тому, кто сделает покупку на сумму более 100 манат, делают скидки 10% от общей стоимости. Сколько должен заплатить покупатель, если купит по одной вещи каждого наименования? 66,1+30,7+41,3+14,2+28,3=180,6-стоит без скидки 180,6*(100-10)/100=180,6*90/100=180,6*0,9=162,54≈162,5
Пошаговое объяснение:
Чтобы дробь достигала минимального значения, числитель должен быть минимален, а знаменатель - максимальным. Заметим, что как в числителе, так и в знаменателе квадратные уравнения относительно a и b, причем в уравнении относительно a, минимальное значение которого нас интересует, коэффициент возле x² больше нуля, следовательно, ветки параболы направлены вверх, и минимальное значение функция принимает в вершине параболы.
В уравнении относительно b ветки параболы направлены вниз, следовательно, максимальное значение достигается так же в вершине параболы.
Вычислим абсциссы вершин парабол по формуле x=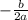 , где a и b - коэффициенты перед x² и x соответственно.
, где a и b - коэффициенты перед x² и x соответственно.
Абсцисса вершины параболы для функции относительно a x=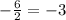 .
.
Значение ординаты в этой точке найдём, подставив полученное значение x в уравнение, получим:
y=9-18+16=7
Проделаем то же для уравнения в знаменателе, получим:
x=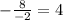
y=5+32-16=21
Минимальное положительное значение дроби: