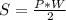, где 
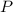— периметр основания, а 
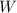— апофема. 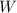в условии дана (6 см), осталось найти периметр основания 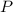. Напомню, что периметр — это сумма длин всех сторон. В основании правильной четырехугольной пирамиды лежит квадрат. У квадрата все стороны равны. Поэтому его периметр найдем по формуле 
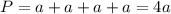, где 
— сторона квадрата. Из условия ясно, что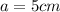 
, отсюда 
.
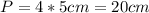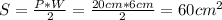. Готово! 
Пошаговое объяснение:
вычислим площадь фигуры с интегралов.
Найдём пределы интегрирования решив уравнение
x^2 + 2x +5 = 5 - 2x
x^2 + 4x = 0
x(x+4) = 0 откуда x=0 , x= -4
S=∫
\int\limits^ -4_0 {(5-x-x^2-2x-5)} \, dx