Лемма: существует такое y-значное число вида XX...X (т.е. состоит из целиком из цифр X) такое, что оно делится на число 1987
Доказательство: число указанного вида можно представить в виде
; Сперва очевидно, что делится на 9. Согласно малой теореме Ферма , так как 1987 - число простое. Так как 9 и 1987 взаимно просты, то число XX...X делится на 1987 для n+1=1986, т.е. для n=1985.
Итак, взяв например n=1985 получим число 1...19...98...86...6, которое раскладывается как , где каждое из чисел вида X...X делится на 1987
ВСПОМИНАЕМ Против течения - скорости складываются, по течению - вычитаются. ДАНО Tпо = 4,5 ч - время по течению. Тпр = 2,1 ч - время против течения. S = 52.2 км - расстояние. Vт = 3 км/ч - скорость течения. НАЙТИ Vл =? - скорость лодки. РЕШЕНИЕ S = 52.2 : 2 = 26.1 расстояние между пунктами. Уравнения движения - S =V/t, V = S/t t= S/V. (Vл - Vт)*Тпр + (Vл + Vт)*Tпо = S Подставляем известные значения, раскрываем скобки и получаем - 4.5*V - 3*4.5 + 2.1*V + 3*2.1 = 52.2 Упрощаем (4,5+2,1)*Vл = 6,6*Vл = 52,2 + 13,5 - 6,3 = 59,4 Vk = 59.4 ^ 6.6 = 9 км/ч - скорость лодки - ОТВЕТ
Лемма: существует такое y-значное число вида XX...X (т.е. состоит из целиком из цифр X) такое, что оно делится на число 1987
Доказательство: число указанного вида можно представить в виде
Итак, взяв например n=1985 получим число 1...19...98...86...6, которое раскладывается как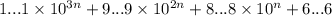 , где каждое из чисел вида X...X делится на 1987
, где каждое из чисел вида X...X делится на 1987