1) (P + 8)² = P² + 16P + 64;
2) (10x - 3y)² = 100x² - 60xy + 9y²;
3) (x - 9)(x + 9) = x² - 81;
4) (4m + 7n) (7n - 4m) = 49n² - 16m²
Пошаговое объяснение:
1) определим уравнение касательной проведенной к графику данной функции в точке с абциссой x₀=2 по формуле y=y₀+y'(x₀)(x-x₀)
y₀=y(2)=2*2-2²=4-4=0 ; y'=2-2x ; y'(2)=2-4=-2
y=-2(x-2)=-2x+4 ; y=-2x+4
2) найдем точки пересечения графиков y=-2x+4 и y=2x-x²
-2x+4=2x-x²
x²-2x+4-2x=0
x²-4x+4=0
(x-2)²=0
x=2
(2;0)
3) найдем точки пересечения графика y=2x-x² с ОХ
y=2x-x²=0
х(2-х)=0
x₁=0 ; x₂=2
4) найдем точкy пересечения графика y=-2x+4 с ОУ
х=0 ; y=-2x+4=-2*0+4=4
(0;4)
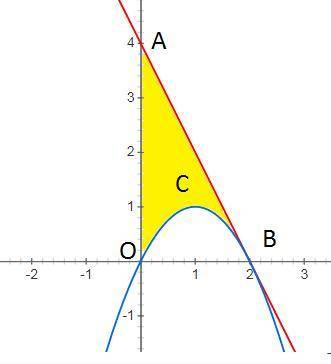
5) схематически построим графики y=-2x+4 и y=2x-x²
6) площадь фигуры ограниченной линиями y=2x-x^2 и касательной проведенной к графику данной функции в точке с абциссой x=2 и с осью ординат
S=SΔOAB-SкриволинейногоΔOCB=
2 2 2
= (OA*OB/2)-∫(2x-x²)dx=(4*2/2)-[(2x²/2)-(x³/3)]=4-[x²-(x³/3)]=
0 0 0
=4-[2²-(2³/3)]=4-[4-(8/3)]=4-4+8/3=8/3=2 2/3
Покрокове пояснення:
1)=р^2+16р+64
2)=100х^2-60ху+9у^2
3)=х^2-81
4)=49n^2-16m^2