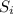, i - это номер стороны (их всего n, их можно занумеровать).
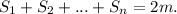. Почему 2m? Потому что в такой сумме значение в каждой вершине будет подсчитано ДВА РАЗА, так как из каждой вершины выходят две стороны.
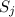будет равно 0. Теперь рассмотрим стороны, на которых написано (1). Их можно также разбить на две группы: те, что соединяют (-1) и (-1), и те, что соединяют (1) с (1). Пусть первых С, а вторых D. Тогда
банка с керос. 350 г;
керос ? г, но в 2 раза легче меда;
банка ? г
Решение:
А р и ф м е т и ч е с к и й с п о с о б.
Если масса меда в банке вдвое больше массы керосина, то можно считать, что в этой банке находится масса меда, равная двойной масса керосина.
500 - 350 = 150 (г) (одна) масса керосина в банке.
350 - 150 = 200 (г) масса пустой банки
ответ: А) 200 г - масса пустой банки.
Проверка: 150*2+200 = 500; 500 = 500
А л г е б р а и ч е с к и й с п о с о б.
Х г масса пустой банки;
(350 - Х) г масса керосина;
2 * (350 - Х ) г масса меда;
(Х + 2 * (350 - Х)) г масса банки с медом;
500 = Х + 2 * (350 - Х) по условию;
500 = Х + 700 - 2Х
Х = 200 (г)
ответ: 200 г масса пустой банки.