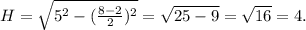
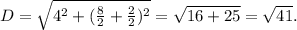
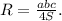
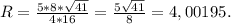
По предыдушему, если числа взаимно просты, то в их разложении нет общих множителей, а это значит, по определению НОК, что он равен их произведению. Если бы это было не так, то это бы значило, что в разложениях множители повторяются, то есть числа не взаимно просты. ответ на задачу 3 - нет (контрпример: 
, хотя они не взамнопросты), на задачу 4 - да.
Да, так как 3 и 4 взаимно просты.
Пошаговое объяснение:
x - ushburish
y - tortburish
x+y = 15 x=15-y
3x+4Y = 53
zamenyaem x
3(15-y) +4y = 53
45 - 3y + 4y = 53
y = 53-45 = 8
x=15-y = 15 - 8 = 7