1) x²−7x−8 < 0
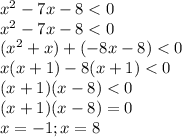
Определяем знаки на промежутках:
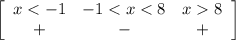
Интервал −1 < x < 8 — удовлетворяет неравенство
Точки выколотые, так как неравенство строгое, — их в ответ не вносим.
ответ: x ∈ (−1; 8).
2) 3x²−4x+7 ≥ 0
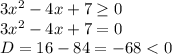
корней нет
делим обе части неравенства на 3х²−4х+7, 3х²−4х+7>0:
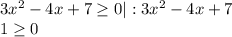
Неравенство выполняется, значит х ∈ R.
ответ: x ∈ (−∞; ∞).
3) x²−2x−3 > 0
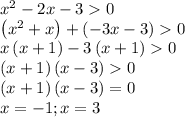
Определяем знаки на промежутках:
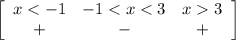
Интервалы x < −1 и x> 3 — удовлетворяют неравенство
Точки выколотые, так как неравенство строгое, — их в ответ не вносим.
ответ: x ∈ (−∞; −1) ∪ (3; +∞).
ответ: 3 ч.
Пошаговое объяснение:
За ней погнался - значит догонял - двигаются в одну сторону.
1) V1 = S1/t1 = 187 : 12 = 15 7/12 м/мин - скорость черепахи
1 км = 1000 м -
2) V2 = S2/t2 = 1000 : 4 = 250 м/мин - скорость Ахиллеса.
3) Vc = V2 - V1 = 250 - 15 7/12 = 234 5/12 м/мин - скорость сближения.
4) T = d/Vc = 42195 : 234 5/12 = 180 мин = 3 ч - время погони - ответ.
Удивительно, что разделилось без остатка.
Черепаха за это время проползла S = V*t = 2 км 805 м