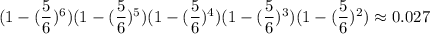Решить: проводник спального вагона (св), собирая билеты у пассажиров, обнаружил, что на два места в некотором купе продано по два билета на каждое место. ответьте, на какие места билеты проданы дважды, в поезде 12 вагонов, в св-вагоне 9 купе, в каждом купе 2 места, а сумма номера вагона (это двузначное число) и всех мест, указанных в билетах, вместе с теми, что проданы дважды, составила 205

👇

Открыть все ответы

Ответ:

Nikikiki303

17.02.2022

Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков

Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда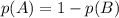 p(A)=1-p(B)

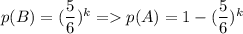Вероятность не угадать число на одном кубике равна $\dfrac{5}{6}$ (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна $p(B)=(\dfrac{5}{6})^k=p(A)=1-(\dfrac{5}{6})^k$ - это и есть искомая вероятность в данной задаче.

Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна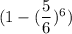 $(1-(\dfrac{5}{6})^6)$ . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна 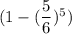$(1-(\dfrac{5}{6})^5)$ . При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна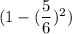 $(1-(\dfrac{5}{6})^2)$

Тогда искомая вероятность $(1-(\dfrac{5}{6})^6)(1-(\dfrac{5}{6})^5)(1-(\dfrac{5}{6})^4)(1-(\dfrac{5}{6})^3)(1-(\dfrac{5}{6})^2)\approx 0.027$

4,7(83 оценок)

Ответ:

edinorogsasha

17.02.2022

1.Решите уравнение:
1)
x + 12 = 7;
x=7-12
x=-5

2)
−13 − x = 7;
x=-13-7
x=-20

3)
3,2 − x = 8;
x=3,2-8
x=-4,8

4)
−0,4x = 8.
x=8:(-0,4)
x=-20

2.Решите уравнение:
1)
6x − 8 = 4x;
6x-4x=8
2x=8
x=8:2
x=4

2)
2х + 3 = x − 5;
2x-x=-5-3
x=-8

3)
3( 6x + 3) = 12x − 3.
18x+9=12x-3
18x-12x=-3-9
6x=-12
x=-12:6
x=-2

3.На двух полках 36 кг книг, причем на одной из них в 3 раза больше чем на другой. Сколько книг было на каждой полке?

3+1=4части
36:4=9книг на одной полке
9*3=27книг на другой полке

4. Три брата собрали 88 кг яблок. Старший собрал в 3 раза больше, чем младший, а средний — на 13 кг больше, чем младший. Сколько килограммов яблок собрал младший брат?

x -собрал младший
3x -собрал старший
x+13 -собрал средний
88кг всего
x+3x+x+13=88
5x+13=88
5x=88-13
5x=75
x=75:5
x=15кг собрал младший

5. Решите уравнение:
1)
17x − 8 = 20x + 7.;
20x-17x=-8-7
3x=-15
x=-15:3
x=-5

2)
8x − 3(2x + 1) = 2x + 4 ;
8x-6x-3=2x+4
2x-3=2x+4
2x-2x=4+3
0 не равно 7
уравнение не имеет корней

3)
0,6(x − 2) + 4,6 = 0,4(7 + x);
0,6x-1,2+4,6=2,8+0,4x
0,6x+3,4=2,8+0,4x
0,6x-0,4x=2,8-3,4
0,2x=-0,6
x=-0,6:0,2
x=-3

6. В двух цистернах было поровну воды. Когда из первой цистерны взяли 54 л воды, а из второй — 6 л, то в первой цистерне осталось в 4 раза меньше воды, чем во второй. Сколько литров воды было в каждой цистерне вначале?

x -в каждой цистерне
x-54 -осталось в первой цистерне
x-6 -осталось во второй цистерне
но известно что в первой в 4раза осталось меньше
составим уравнение

4(x-54)=x-6
4x-216=x-6
4x-x=-6+216
3x=210
x=210:3
x=70литров воды было в каждой цистерне

7. Решите уравнение
(3x + 42)(4,8 − 0,6x) = 0

3x+42=0 4,8-0,6x=0
3x=-42 0,6x=4,8
x=-42:3 x=4,8:0,6
x=-14 x=8

ответ: -14 ; 8.

4,7(25 оценок)

Это интересно:

Хобби-и-рукоделие

24.08.2021

Как сшить детское платье: пошаговая инструкция...

Питомцы-и-животные

06.11.2020

Как убить муху: 5 действенных способов...

Кулинария-и-гостеприимство

17.08.2020

Шоколадная водка: рецепты домашнего приготовления...

Стиль-и-уход-за-собой