Объяснение:
1. Смотрим на первую цифру - 8, она делится на 4 => делим 8 на 4 и получаем 2 => записываем 2 в ответ как 1 цифру результата
2. Следующая цифра 4, она делится на 4, делим как восьмерку и получаем 1, записываем 1 в ответ после двойки
3. Далее берем цифру 1, она не делится на 4 (получается не целое число, то есть меньше 1, такое число нельзя вписывать в столбик счисления, можно просто запутаться и посчитать неправильно, и тем более когда проходят деление в столбик, по-моему ребята даже не знают о таких числах), пишем 0 после числа 1 в ответе, поэтому вместе с единичкой (которая в столбике счисления) берем следующую цифру - 2, получается в столбике 12, оно делится на 4 и получаем 3, пишем 3 после нолика
4. Теперь берем цифру 4, она делится на 4 и получаем 1, пишем ее после тройки в ответе
5. Остается 0, если в конце числа стоит 0 (круглое число), то мы переносим этот нолик в ответ, получаем наш ответ: 210310
Могут быть случаи, когда при делении числа в столбике счисления получается остаток, мы его берем вместе со следующей цифрой, как в случае с цифрой 12 (3 номер)Пример деления в столбик есть на фотографии нижеТакже НУЖНО АККУРАТНО ПИСАТЬ В ТАКИХ СТОЛБИКАХ, ведь из-за неаккуратности можно запутаться и решить неправильноНолики, например, перед цифрой 8 лучше не писать, это я так считаюЯ надеюсь, что я Вам и Вы разобрались)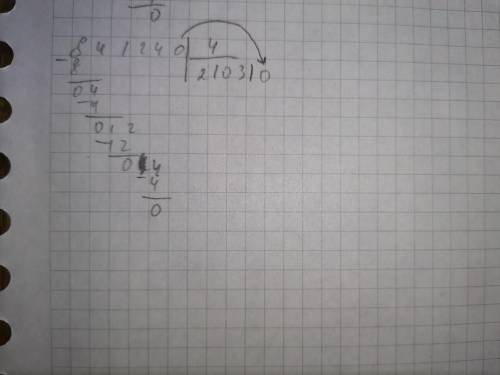
2f(x), а, значит, и функция f(x).
Пошаговое объяснение:
Мы воспользуемся следующими свойствами непрерывных функций:
(1) сумма и разность непрерывных функций — непрерывные функции;
(2) если g(x) — непрерывная функция, функция g(ax) также непрерывна.
Теперь заметим, что по условию непрерывны функции f(x) + f(2x) и f(x) + f(4x), а в силу свойства (2) вместе с функцией f(x) + f(2x) непрерывна и функция f(2x) + f(4x).
Далее, по свойству (1) непрерывна функция (f(x) + f(2x)) + (f(x) + f(4x)) – (f(2x) + f(4x)) = 2f(x), а, значит, и функция f(x).