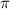
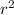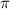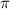= 4 дм * 4 дм * = 16. Так как основание треугольника это диаметр конуса, то для радиуса мы берём половину.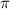*h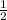
AC = 4, получается, что AB = 
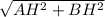. Получается, что BH = 
= 
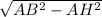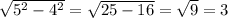
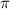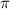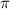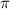
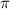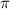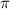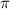
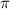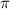* h = 16 * BH = 16 * 3 = 48rl, где l — образующая. * AB * AH = * 5 * 4 = 20 + 20 = 36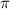
Формула объёма конуса: S основания * h (высота).
S основания =
V конуса = 16
Данный нам равнобедренный треугольник ABC, в котором AC — основание, — 8 дм, а AB = BC. Получается, что P треугольника ABC = 2AB + AC, из чего следует, что 2 AB = P треугольника - AC = 18 - 8 = 10. AB = BC = 5.
По теореме Пифагора находим высоту конуса. Из треугольника ABH, в котором AB = 5, AH =
Возвращаемся к формуле. V конуса = 16
S полной поверхности конуса = S основания + S боковой поверхности.
S боковой поверхности =
l = AB = 5, r = AH = 4
S боковой поверхности =
S полной поверхности = 16