777 литра
Пошаговое объяснение:
Пусть в 1-сосуде Х литр воды, а во 2-сосуде 0 литр воды.
1-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 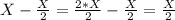
2-сосуд: 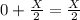
Объем воды в обоих сосудах в сумме дают Х литр!
2-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 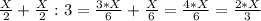
2-сосуд: 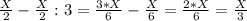
Объем воды в обоих сосудах в сумме дают Х литр!
3-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 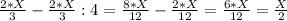
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
Теперь покажем, что в нечётных числах переливания всегда
1-сосуд: 
2-сосуд: 
Пусть n=2·k+1.
n-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 
2-сосуд: 
(n+1)-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 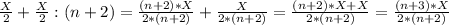
2-сосуд: 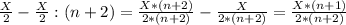
(n+2)-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 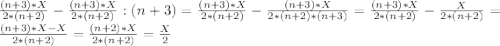
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
что требовалось показать.
Отсюда, 2019 - нечётное и X=1554 литра, тогда
1-сосуд: 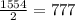
Q =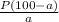
Пошаговое объяснение:
a=(1-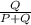 )*100
)*100
1-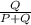 =
=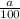
aP+aQ=100P
aQ=100P-aP
Q=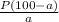
Все верно. Возможно, что ты сам что-то в задании пропустил, но данное выражение точно верно.