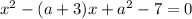
Воспользуемся теоремой Виета:
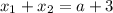
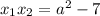
Произведение корней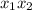 
на 2 больше суммы 
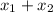этих корней, следовательно:
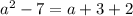
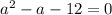
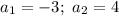
Определим, при каких значениях параметра 
данное уравнение существует.
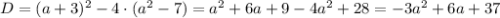
Следовательно,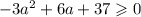 
— условие существования корней данного квадратного уравнения.
Проверим, удовлетворяют ли полученные значения параметров для решения исходного уравнения.
Если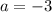 
, то получаем неправильное неравенство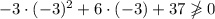 
Если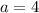 
, то получаем верное неравенство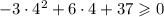 
Таким образом, только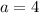 
обратит данное уравнение в таковое, что произведение корней на 2 будет больше суммы этих корней.
ответ: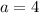
Р(А)=0,5
Р(В)=0,375
Р(С)=0,25
Пошаговое объяснение:
Вероятность события Р=m/n, где n - общее число исходов, m - благоприятное число исходов.
При бросании монеты равновероятно выпадение герба и решки.
Монета бросается три раза. При этом возможны следующие исходы:
ггг, ггр, грг, грр, ррр, ррг, ргр, ргг
n=8
Событие А: "Число выпадения герба больше числа выпадения решки"
m=4 (ггг, ггр, грг, ргг)
Р(А)=4/8 = 0,5
Событие В: "Выпадает два герба"
m= (ггр, грг, ргг)
Р(В)=3/8=0,375
Событие С: "Результаты всех бросаний одинаковы"
m=2 (ггг, ррр)
Р(С)= 2/8=0,25