Аличие единичного элемента N = 1 (Множество натуральных чисел имеет как минимум 1 элемент) Наличие функции S(N) такой, что S(N) всегда принадлежит N (Для каждого элемента есть задать минимум один соседний элемент) Отсутствие элементов, таких что S(N) = 1 (Для единичного ровно один) Отсутствие элементов, таких что для элементов N1,N2 S(N1) = S(N2) (Для прочих не более двух, и этот однозначен для всех элементов N) Отсутствие элементов, таких что зависящий от элемента N предикат P(N) ложен если P(1), P(N) и P(S(N)) истинны. (Прочие же свойства натуральных чисел одинаковы, какие бы натуральные числа мы не брали, и какие бы их свойства не исследовали
Из условия следует, что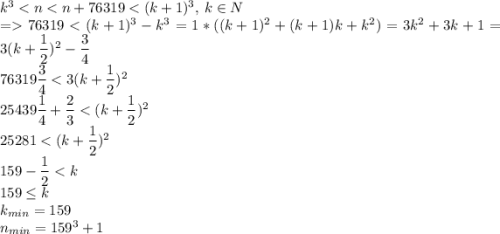
Проверим: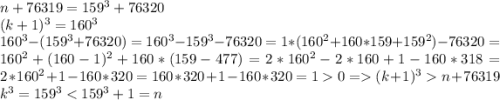
Верно.
ответ: