18 карточек
Пошаговое объяснение:
Найдём количество чисел которые делятся на 2 с арифметической прогрессии.
Пусть a₁ = 10, aₙ = 48, d = 2 и нам необходимо найти n
Воспользуемся формулой: aₙ = a₁ + (n-1)·d
Выразим из этой формулы n:
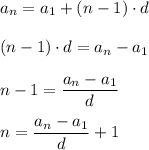
Подставим известные данные и найдём n:

Значит в данном наборе содержится 20 чисел, которые делятся на 2
Количество чисел которые делятся на 7 в данном наборе не так много и их можно просто перечислить.
На 7 делятся числа 14, 21, 28, 35, 42 и 49 - всего 6 чисел.
Но числа 14, 28 и 42 мы уже учли, так как они делятся на 2.
Поэтому количество чисел, которые делятся на 2 или 7 равно:
20 + (6 - 3) = 20 + 3 = 23 числа
Следовательно, количество чисел, которые не делятся на 2 или 7 равно 40 - 23 = 17 чисел
Мы можем взять не глядя 17 карточек, но все числа на них могут не делиться на 2 или 7, но если мы возьмём ещё как минимум одну карточку, то мы найдём как минимум одно число, которое делится на 2 или 7.
1-Задание.
35+(-11)=35-11=24
-22+(-15)=-22-15=-39
25+(-39)= 25-39=-14
-33+(-42)= -33-42= -75
2-Задание.
35-(-11)= 35+11=46
-22-(-15)= -22+15= -7
25-(-39)=25+39= 64
-33-(-43)= -33+43= 10
3- Задание.
42+(-16)= 42-16= 26
-37-(-62)= -37+62= 25
-17+(-52)= -17-52=-69
-39-35= -74
422+(-26)-(-36)= 422-26+36= 432
-465-(-47)+(-27)=-465+47-27= -445
-125+125-(-5)=-125+125+5=5
-38-(-38)-4= -38+38-4= 4
Почему в двух последних выражении стоит ответ : 5 и 4 ?
Потому что Сумма двух противоположных чисел равна нулю...
Пример :
-3+3=0
ответ : 0;
5-Задание.
Тут я бессилен ( ничего не понимаю) ;(