Даны уравнения: 3y^2=25x, 5x^2=9y.
Выразим их относительно у: y=5√x/√3, y = 5x^2/9.
Чтобы определить границы заданной фигуры, надо приравнять правые части полученных уравнений:
5√x/√3 = 5x^2/9. Сократим на 5: √x/√3 = x^2/9. Возведём обе части в квадрат: х/3 = х^4/81 или 81х = 3x^4. Сократим на 3: 27х = x^4.
Перенесём всё влево: 27х - x^4 = 0 или х(27 - x^3) = 0.
Отсюда получаем 2 точки пересечения графиков заданных функций, которые и есть границами фигуры, площадь которой надо определить.
х = 0 и х = ∛27 = 3.
Теперь определяем площадь этой фигуры как интеграл разности:
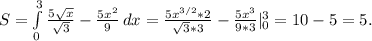

4 + 4√3 см.
Пошаговое объяснение:
Начертим рисунок к задаче:
А - точка, отстоящая от плоскости на расстоянии 4 см,
АН - перпендикуляр из точки А на плоскость, его длина 4 см,
АВ - наклонная из точки А, образующая угол 30° с плоскостью,
АС - наклонная из точки А, образующая угол 45° с плоскостью,
угол между наклонными АВ и АС прямой.
Так как АН перпендикуляр, то треугольники АНВ и АНС прямоугольные.
В треугольнике АНС один из острых углов равен 45°, следовательно два его катета АН и НС равны между собой, таким образом НС = 4 см.
tg ABH = АН/HВ;
HB = AH/tg ABH = 4/tg 30° = 4/(1/√3) = 4√3 (см).
Расстояние между концами наклонных будет равно сумме отрезков ВН и НС:
ВС = ВН + НС = 4 + 4√3 (см).
ответ: 4 + 4√3 см.