ответ: во вложении пошаговое объяснение:

Наполненный бассейн примем за единицу (целое).
1) 1 : 15 = 1/15 - часть бассейна, которая наполнится через первый кран за 1 час;
2) 1 : 12 = 1/12 - часть бассейна, которая наполнится через второй кран за 1 час;
3) 1 : 8 = 1/8 - часть бассейна, которая наполнится через третий кран за 1 час;
4) 1/15 + 1/12 + 1/8 = 8/120 + 10/120 + 15/120 = 33/120 - часть басейна, которая наполнится через все три крана за 1 час;
5) 1 : 33/120 = 1 · 120/33 = 120/33 = 40/11 = 3 7/11 ч - время наполнения бассейна.
ответ: за 3 целых 7/11 ч (≈3 ч 38 мин).
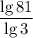 1) По формуле перехода к новому основанию
1) По формуле перехода к новому основанию 
в данном случае а = 3, b = 81, c = 10
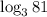
 3) Вынесем степень как множитель
3) Вынесем степень как множитель 
в данном случае а = 3, b = 3, c = 4

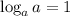
в данном случае а = 3

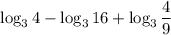 1) По формуле
1) По формуле 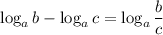
в данном случае а = 3, b = 4, c = 16
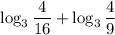

в данном случае а = 3, b = 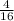 , с =
, с = 
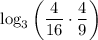
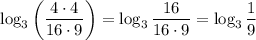 4) Заменим
4) Заменим  на 3⁻²
на 3⁻²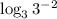 5) Вынесем степень как множитель
5) Вынесем степень как множитель 
в данном случае а = 3, b = 3, c = -2
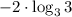
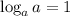
в данном случае а = 3
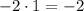
 1) Занесем множитель как степень
1) Занесем множитель как степень 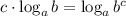
в данном случае c = 2, a = 7, b = 27
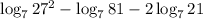
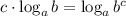
в данном случае c = 2, a = 7, b = 21
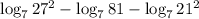
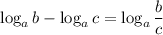
в данном случае а = 7, b = 27², c = 81
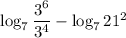
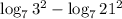 6) По формуле
6) По формуле 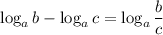
в данном случае а = 7, b = 3², c = 21²

 8) Заменим
8) Заменим 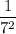 на 7⁻²
на 7⁻²

в данном случае а = 7, b = 7, c = -2
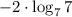
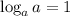
в данном случае а = 7
P.S. Использовались формулы замены бесконечно малых величин эквивалентными бесконечно малыми.