1) 15 см и 18 см
2) 75√3 см²
Пошаговое объяснение:
1) Площадь прямоугольника вычисляется по формуле S = a • b, где a и b стороны прямоугольника.
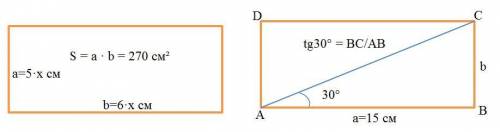
Пусть х>0 коэффициент пропорциональности. Тогда одна сторона прямоугольника равна a=5•х см, а вторая b=6•х см (см. рисунок). Подставляем в формулу площади и найдём х:
5•х см•6•х см =270 см²
30•х² см²= 270 см²
х²=270:30
x²=9
x=3
Значит, одна сторона a=5•3 см=15 см, другая сторона b=6•3 см = 18 см.
2) Площадь прямоугольника вычисляется по формуле S = a • b, где a и b стороны прямоугольника. По условию a=AB= 15 см, определим b=BC. Диагональ AC делить прямоугольник ABCD на прямоугольные треугольники ABC и ADC (см. рисунок). В треугольнике ABC по определению
tg30° = BC/AB = b/a или b = a• tg30° = 15 см • √3/3=5√3 см.
Тогда S = 15 см • 5√3 см = 75√3 см².
ответ: 90 звонков .
Вначале представим, что каждый разговаривал с каждым по одному разу (для того, чтобы получить окончательный ответ, будет достаточно умножить полученное число на 6). Возьмем любого из шестиклассников. Естественно предположить, что, разговаривая по одному разу с остальными шестиклассниками, он разговаривал (звонил или отвечал на звонки) всего 6 - 1 = 5 (раз). Так как всего шестиклассников 6, то и звонков 6 * 5 = 30. Но, заметим, что когда Вася разговаривал с Петей, а Петя разговаривал с Васей, - это один звонок, поэтому мы каждый звонок посчитали дважды, и нужно разделить результат на 2. Поэтому поделим 30 еще на 2, и получим 15.
Но так как каждый разговаривал с каждым по 6 раз, то всего было звонков: 15 * 6 = 90. Задача решена!