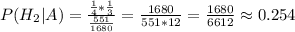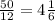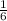, 
нам "говорит" о том, что это следующий подъезд, 4 подъезда по 12 квартир получается 48, а т.к. Глеб живет в 50 квартире, то это уже сдедующий подъезд, т.е. 5. А т.к. квартир на каждом этаже по 3, то следовательно получаем те 2 квартиры, которые остались находятся на 1 этаже. ответ: Глеб живет в 5 подъезде на 1 этаже
≈ 0.254
Пошаговое объяснение:
Пусть имеются следующие гипотезы:
H₁ - студенту попался вопрос на билет из 1 темы
H₂ - студенту попался вопрос на билет из 2 темы
H₃ - студенту попался вопрос на билет из 3 темы
H₄ - студенту попался вопрос на билет из 4 темы
Соответственно априорные вероятности тогда равны P(H₁)=P(H₂)=P(H₃)=P(H₄) =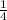 
Пусть событие A связано с тем, что студент не ответил на вопрос. Тогда условные вероятности равны:
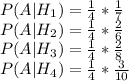
А полная вероятность (т.е. вероятность того, что студент не сдал экзамен) равна сумме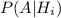 
по всем i.
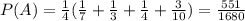
Находим теперь апостериорную вероятность, согласно формуле Байеса:
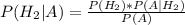
Таким образом,
