ответ: (√х-6)²-1=0 равносильно уравнению 2x-6√x=6√x+x-35.
Объяснение:
Два уравнения будут равносильными, если они имеют одно и то же множество корней (в случае кратных корней кратности соответствующих корней должны совпадать.)
Решим данное уравнение.
2x-6√x=6√x+x-35; x-12√x+35=0, по Виета √х=5⇒х=25; √х=7⇒х=49, т.е. данное уравнение имеет два корня 25 и 49.
Проверим сначала, являются ли эти корни корнями оставшихся уравнений. 1) (√25+5)²-1=0, т.к. 99≠0, то второй корень можно и не проверять.
2) √(25+6)²-1=0; т.к. 120≠0, второй корень тоже не проверяем.
3) т.к. при переносе вправо единицы получим (√х+6)²=-1, чего быть не может, то это уравнение вообще не имеет корней.
Т.е. первые три уравнения не равносильны данному. Проверим четвертое.
4) (√25-6)²-1=0; 0=0; ( √49-6)²-1=0; 0=0- верное равенство. Значит, корни четвертого уравнения являются корнями первого. Других корней у последнего уравнения нет , т.к. (√x-6)²-1=0 можно упростить , получим
х-12√x+36-1=0;х-12√x+35=0- а это и есть первое уравнение.
Вывод четвертое уравнение равносильно уравнению, данному в условии задачи.
Общий вид аналитической функции выглядит так
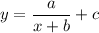
теперь по порядку
с- сдвиг функции у= 1/х по оси Оу. Мы видим что смещение на 1 единицу вверх, значит с= +1
b - сдвиг функции 1/x по оси Ох. Мы видим что движение на 2 единицы в право. Значит b = -2 ( Минус из-за того что раньше при х=0 не было решений, теперь при х=2 нет решений, тогда х-2)
а- это к/т растяжения.
Определяем так: смотрим на новый график с новыми осями (старые оси "пропали") и смотри при х=1 у= -1 тогда а/1= -1, значит а= -1
И теперь все это подставляем
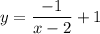
начни с алгебрический дробей
Объяснение:
или с обычных а потом перехрди дальше, совет