034х=-374
х=-012
Объяснение:
сначала переносим иксы в одну сторону, а числа в другую и считаем
(1) -2⁷*-2²=-2⁹ (если основания равны(в нашем случае они равны=-2), то при умножении степени складываются)
2) (-х³)²*х⁴ (если у тебя такая ситуация, что число в скобках в степени, а после скобки ещё степень (-х³)² , то степени перемножаются и в нашем случает, это будет -х⁶, но чтобы воспользоваться правилом тем, которое мы использовали в первом выражении(1), нам нужно заметить, что -х⁶ находится в чётной степени, а это значит, что каким бы не был х, выражение -х⁶ будет положительным, значит -х⁶=х⁶, что бы у нас получилось, мы должны в уравнении использовать х⁶, что бы было одинаковое основание, используем:
х⁶*х⁴=х¹⁰
Числа при делении на 9 могут давать остатки 0,1,2,3,4,5,6,7,8,9. поєтому любое натуральное число можно записать в виде
n=9m+r, где m - некоторое неотрицательное число, r - цифра
Используя формулу куба суммы
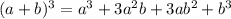
видим, что остаток от деления числа n^3 такой же как у числа b^3, так как
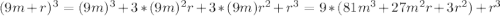
Рассмотрим остатки от деления кубов одноцифровых чисел
Кубы одноцифровых чисел 0, 1, 8, 27, 64, 125, 216, 343, 512, 729.
Числа 0, 27, 216, 729 при делении нацело на 9 дают остаток 0
Числа 1, 64, 343 при делении нацело на 9 дают в остатке 1
Числа 8, 125, 512 при делении нацело на 9 дают в остатке 8.
Таким образом делаем вывод, что кубы натуральных чисел при делении на 9 могут давать только остатка 0,1 и 8.
Доказано
1100
Объяснение:
0,71х+198=0,37-176
0,71х-0,37х=-176-198
0,34х=374
х=374:0,34
х=1100