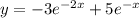ответ: во вложении Объяснение:

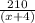 часов -потребуется теплоходу на путь в один конец.
часов -потребуется теплоходу на путь в один конец.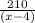 часов -потребуется теплоходу, чтобы вернуться после стоянки.
часов -потребуется теплоходу, чтобы вернуться после стоянки.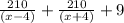 часов - общее время теплохода в пути туда-обратно или это 27 часов как дано в условии.
часов - общее время теплохода в пути туда-обратно или это 27 часов как дано в условии.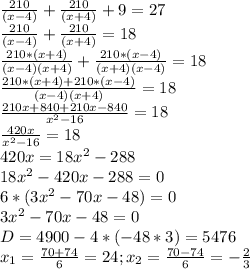
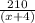 часов -потребуется теплоходу на путь в один конец.
часов -потребуется теплоходу на путь в один конец.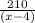 часов -потребуется теплоходу, чтобы вернуться после стоянки.
часов -потребуется теплоходу, чтобы вернуться после стоянки.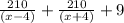 часов - общее время теплохода в пути туда-обратно или это 27 часов как дано в условии.
часов - общее время теплохода в пути туда-обратно или это 27 часов как дано в условии.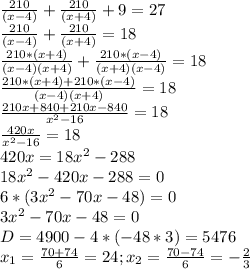
Найти частное решение дифференциального уравнения:
y''+3y'+2y=0, y(0)=2, y'(0)=1
Данное дифференциальное уравнение является однородным. Перейдем к характеристическому уравнению, выполнив замену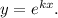
Общее решение дифференциального уравнения:
Найдем теперь частное решение нашего диф. уравнения
Подставим начальные условия
Сложив обе уравнения, получим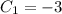 , тогда
, тогда 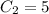
Частное решение: