Запишем эту сумму для произвольного числа слагаемых:
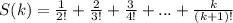
Вычислим значения S(k) для нескольких значений k:
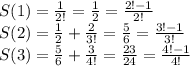
Тогда можно предположить, что
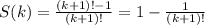
Но это ещё надо доказать. Используем индукцию. Выше было показано, что равенство верно для первых 3 натуральных k. Докажем, что из справедливости равенства для k=n следует справедливость равенства для k=n+1, тогда равенство можно будет считать справедливым для всех натуральных k.
Итак, предположим, что справедливо равенство
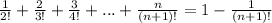
Проверим, верно ли, что
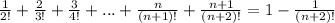
Подставляем сюда предыдущее выражение:
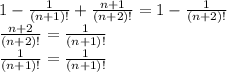
Получили верное равенство. Теперь можно вычислить значение нашей суммы:
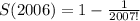
Пусть одно из слагаемых равно x. Тогда второе равно 5-x. Произведение, о котором говорится в условии задается формулой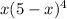 
. Нам нужно найти x, для которого это выражение оказывается наибольшим. То есть фактически нужно найти точку максимума функции 
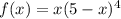на интервале (0; 5).
Возьмём производную:
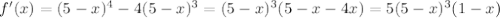
На заданном интервале производная имеет единственный ноль: точку x=1. При этом: f(0)=f(5)=0, f(1)=256. Значит x=1 - точка максимума на интервале (0; 5).
1 это первое слагаемое. Тогда второе, очевидно, равно 4.
ответ: 1 и 4
((1+3)*5+2)*2+5=49
Пошаговое объяснение:
1+3=4
4*5=20
20+2=22
22*2=44
44+5=49