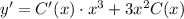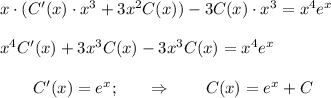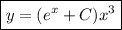
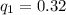 - вероятность выхода прибора из строя при нормальном режиме
- вероятность выхода прибора из строя при нормальном режиме
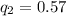 - вероятность выхода прибора из строя в условиях перегрузки
- вероятность выхода прибора из строя в условиях перегрузки
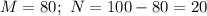
Значит, нормальный режим полета длится 80 % всего времени полета, а условия перегрузки - 20 %.
Вероятность того, что случайно выбранный момент времени полета соответствует нормальному режиму:
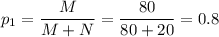
Тогда, вероятность того, что случайно выбранный момент времени полета соответствует условиям перегрузки:
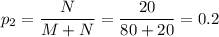
Вероятность того, что прибор выйдет из строя при нормальном режиме:
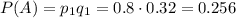
Вероятность того, что прибор выйдет из строя в условиях перегрузки:
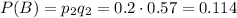
Так как выход из строя при нормальном режиме и выход из строя в условиях перегрузки - несовместные события, то вероятность выхода прибора из строя в полете равна сумме двух вероятностей:
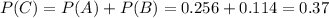
Надежность есть вероятность противоположного события, то есть вероятность того, что прибор не выйдет из строя в полете:
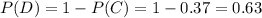
ответ: 0.63
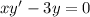 (*)
(*)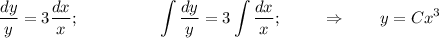
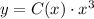 . Тогда, дифференцируя по правилу произведения.
. Тогда, дифференцируя по правилу произведения.