Объяснение:
Уравнение касательной имеет вид:
y=f(x_0)+f'(x_0)(x-x_0)y=f(x
0
)+f
′
(x
0
)(x−x
0
)
Дана функция:
f(x)=-x^2-4x+2f(x)=−x
2
−4x+2
Найдём значение функции в точке x₀:
f(x_0)=f(-1)=-(-1)^2-4 \cdot (-1)+2=-1+4+2=5f(x
0
)=f(−1)=−(−1)
2
−4⋅(−1)+2=−1+4+2=5
Найдём производную функции:
f'(x)=-2x^{2-1}-4=-2x-4f
′
(x)=−2x
2−1
−4=−2x−4
Найдём производную функции в точке x₀:
f'(x_0)=f'(-1)=-2 \cdot (-1) -4 =2-4=-2f
′
(x
0
)=f
′
(−1)=−2⋅(−1)−4=2−4=−2
Подставим найденные значения, чтобы найти уравнение касательной:
y=f(x_0)+f'(x_0)(x-x_0)y=f(x
0
)+f
′
(x
0
)(x−x
0
)
y=5+(-2)(x-(-1))y=5+(−2)(x−(−1))
y=5-2(x+1)y=5−2(x+1)
y=5-2x-2y=5−2x−2
\boxed{y=-2x+3}
y=−2x+3
ответ: y=-2x+3 - искомое уравнение.
1) Коэффициент равен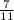 , а степень многочлена равна 8.
, а степень многочлена равна 8.
2) PΔ=7xy³+8x-4y. Степень многочлена равна 4.
3) 4х²+4хz+3x+3z=(x+z)*(4х+3)
Объяснение:
1) Коэффициент при многочлене узнать просто: это вещественное число, стоящее перед множителями хᵃ и уᵇ. Где a, b - степени множителей соответственно х и у. В данном случае коэффициент равен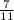 . Теперь, чтобы узнать степень одночлена, надо сложить степени при х и у:
. Теперь, чтобы узнать степень одночлена, надо сложить степени при х и у:
7(степень при х)+1(степень при у)=8.
8 - степень данного одночлена.
2) PΔ=a+b+c=2xy³+3xy³+6x-4y+2xy³+2x=5xy³+6x-4y+2xy³+2x=5xy³+2xy³+6x-4y+2x=7xy³+6x-4y+2x=7xy³+8x-4y.
Степень этого многочлена можно узнать по первому члену. То есть 1 (степень у множителя х)+3(степень у множителя у)=4
3) 4х²+4хz+3x+3z=4x*(x+z)+3*(x+z)=
выносим за скобку множитель (x+z). Получаем
=(x+z)*(4х+3)