В рассматриваемом шестиразрядном числе abcdef, разряд “a” может принимать значения от 1 до 9 (9 значений), разряд “b” может принимать значения от 0 до 0 (1 значение), разряд “c” может принимать значения от 0 до 9 (10 значений), разряд “d” может принимать значения от 0 до 9 (10 значений), разряд “e” может принимать значения от 4 до 4 (1 значение), разряд “а” может принимать значения от 0 до 9 (10 значений).
Посчитаем всевозможное количество значений, которое может принимать число abcdef.
N=9*1*10*10*1*10=9000
Точно также посчитаем всевозможное количество значений, которое может принимать четырехзначное число wxyz, у которого разряд “w” может принимать значения 1 до 9 (9 значений), разряд “x” может принимать значения от 0 до 9 (10 значений), разряд “y” может принимать значения от 0 до 9 (10 значений), разряд “я” может принимать значения от 0 до 9 (10 значений).
M=9*10*10*10=9000
Как видим M=N. Число шестизначных чисел с двумя неизменяемыми разрядами равно числу четырехзначных чисел.


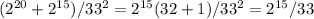
Объяснение:
Показываю, как я понял из твоей подачи эти выражения, а заодно внимательней вглядись и не перепутаешь, где числитель, где знаменатель, и что на что делить и умножать:
((a-2)/(a+2) -(a+2)/(a-2))÷(12a²/(4-a²))=((a-2)(a-2)-(a+2)(a+2))/((a+2)(a-2)) ·(2-a)(2+a)/(12a²)=(a²-2a-2a+4-a²-2a-2a-4)/(a-2) ·(a-2)/(-12a²)=-8a/(-12a²)=2/(3a)
(8x/(x-2) +2x)÷(4x+8)/(7x-14)=(8x+2x(x-2))/(x-2) ·7(x-2)/(4(x+2))=7x(8+2x-4)/(4(x+2))=7x(4+2x)/((4(x+2))=14x(2+x)/(4(x+2))=7x/2