1. ОТВЕТ: например, 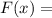
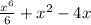 , поскольку
, поскольку 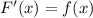 .
.
Общий вид первообразных - 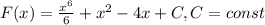
2. Докажем, что 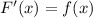 :
:
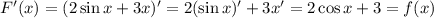 .
.
Что и требовалось доказать.
3. Общий вид первообразных функции 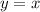 -
- 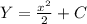 , где
, где 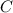 - некоторое постоянное число. Если график первообразной проходит через точку
- некоторое постоянное число. Если график первообразной проходит через точку 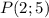 , то это значит, что при подстановке
, то это значит, что при подстановке 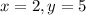 получим верное равенство:
получим верное равенство:
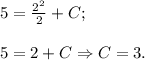
Искомая первообразная - 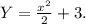
ОТВЕТ: Y = x²/2 + 3.
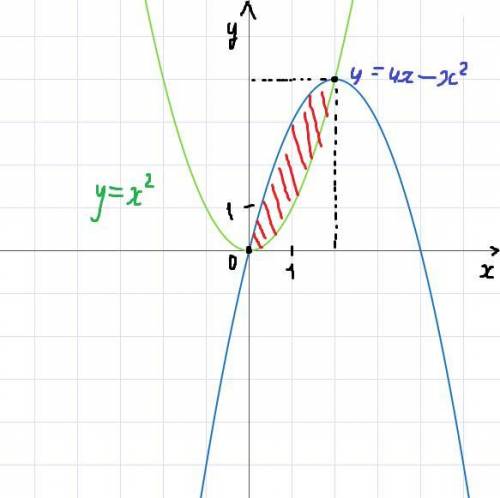
4. Графики функции - во вложении 1. Площадь заданной фигуры заштрихована красным.
Поскольку график функции y = 4x - x² на отрезке [0; 2] располагается как минимум не ниже графика функции y = x² (выполняется неравенство 4x - x² ≥ x²), то площадь будет иметь вид
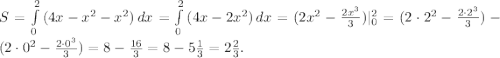
ОТВЕТ: 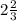 кв. ед.
кв. ед.
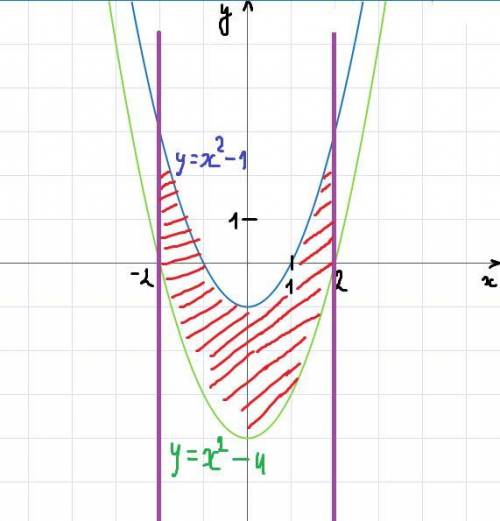
5. Графики - во вложении 2. Площадь заданной фигуры заштрихована красным.
Поскольку на отрезке (-2; 2) график функции y = x² - 1 располагается выше графика функции y = x² - 4 (выполняется равенство x² - 1 > x² - 4), то площадь будет иметь вид
![S=|\int\limits^2_{-2} {[x^2-1-(x^2-4)]} \, dx |=\int\limits^2_{-2} {3} \, dx= (3x)|_{-2}^2=3\cdot2-[3\cdot(-2)]=6+6=12](/tpl/images/1179/2526/6e4c7.png)
ОТВЕТ: 12 кв. ед.
6. Объем выполненной работы A(t) с момента 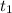 по момент
по момент 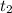 согласно механическому смыслу определенного интеграла есть значение выражения интеграла
согласно механическому смыслу определенного интеграла есть значение выражения интеграла
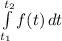
Имеем:
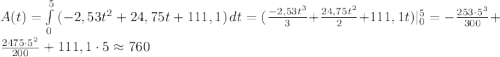
ОТВЕТ: ≈ 760.
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо:
1) В формулу функции вместо y подставить x, вместо x — y:
x=f(y).
2) Из полученного равенства выразить y через x:
y=g(x).
Пример.
Найти функцию, обратную функции y=2x-6.
1) x=2y-6
2) -2y=-x-6
y=0,5x+3.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.
\[\begin{array}{l} y = 2x - 6\\ \begin{array}{*{20}{c}} x&\vline& 0&\vline& 3\\ \hline y&\vline& { - 6}&\vline& 0 \end{array} \end{array}\]