Все .чтобы перевести значение температуры по шкале цельсия в шкалу фаренгейта, пользуются формулой tf=1,8tc+32, где tc — температура в градусах цельсия, tf —температура в градусах фаренгейта. скольким градусам по шкале фаренгейта соответствует −25 градусов по шкале цельсия?

👇

Увидеть ответ

Ответ:

Иван66665

02.05.2022

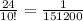
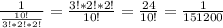
Просто подставь в уравнение tC= -25

Получится:

tF=1,8*(-25)+32

tF=45+32=77

tF=77 — ответ

4,8(34 оценок)

Ответ:

nadj5555

02.05.2022

tF=1,8×tC+32=

tF=1,8×25+32=

=45+32

=77

4,8(82 оценок)

Открыть все ответы

Ответ:

Марк2992

02.05.2022

Букв у нас 10, 3 буквы А, по 2 буквы М и Т, и по одной Е, И и К.
На первую позицию можно ставить одну из десяти букв, на вторую, одну из девяти и т.д. Получим: 10!
Найдём количество которыми можно составить слово математика из данного набора букв при учёте позиции той или иной буквы.
Е, И и К могут занимать только одну позицию, а вот А, М и Т можно менять местами.
Для М и Т это будет 2! и 2!, для А – 3!
С учётом порядка позиции их будет: 1*1*1*2!*2!*3! = 24

Тогда вероятность (согласно классическому определению): $\frac{24}{10!} = \frac{1}{151200}$

Попробуем другой, более простой
Перестановки с повторением.
Всего у нас $\frac{(1 + 1 + 1 + 2 + 2 + 3)!}{3!*2!*2!} = \frac{10!}{3!*2!*2!}$
Перестановка с повторением, которая даёт нам слово "Математика" всего одна, потому мы получаем вероятность:
$\frac{1}{\frac{10!}{3!*2!*2!}} = \frac{3!*2!*2!}{10!} = \frac{24}{10!} = \frac{1}{151200}$

4,6(93 оценок)

Ответ:

Егор4ik18

02.05.2022

Cos²x -cosx -2 > 0 ; * * * замена   cosx =t ; |t|≤1 * * *
t² -t -2 >0 ;
(t+1)(t -2) >0 ;
+ - +
(-1) 2

t∈( -∞ ; -1) U (2 ; ∞) . ⇒ cosx ∈ ( -∞ ; -1) U (2 ; ∞) невозможно .

ответ: x ∈ ∅ .

sin²x - 2sinx -3 < 0 ;  замена  sinx =t ; |t|≤1 * * *
t² -2t -3 < 0 ;
(t+1)(t -3) <0 ;
+    - +
(-1) 3
t∈( -1;3) ⇒ sinx   ∈ ( -1; 3) учитывая что sinx ≤1 получается
sinx   ∈ ( -1; 1] .

ответ:   для всех  x ≠ - π/2 +2πk , k∈Z.

x ∈ R  \ {. -π/2 +2πk , k∈Z }

4,6(88 оценок)

Это интересно:

Кулинария-и-гостеприимство

28.09.2021

Шаг за шагом: Как пользоваться штопором и открыть бутылку вина...

Компьютеры-и-электроника

09.10.2022

Как сделать стекло в игре Minecraft: подробный гайд...

Здоровье

14.01.2023

Очистка организма от кокаина: научно проверенные методы...

27.05.2020