1)
ОДЗ: 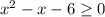 ⇒
⇒ 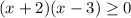 ⇒
⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
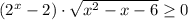 ⇔
⇔
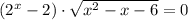 или
или 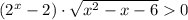
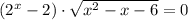 ⇒
⇒ 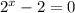 или
или 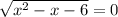 ⇒
⇒
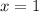 или
или  или
или 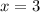
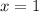 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 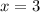
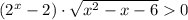 при
при ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
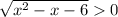 , тогда
, тогда 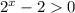 ⇒
⇒ 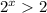 ⇒
⇒ 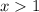
C учетом ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png) получаем ответ:
получаем ответ:
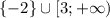
2)
ОДЗ: 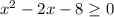 ⇒
⇒ 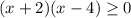 ⇒
⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
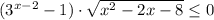 ⇔
⇔
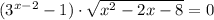 или
или 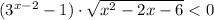
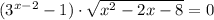 ⇒
⇒ 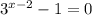 или
или 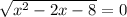 ⇒
⇒
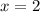 или
или  или
или 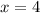
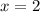 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 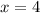
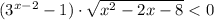 при
при ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
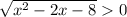 , тогда
, тогда 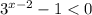 ⇒
⇒ 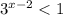 ⇒
⇒ 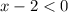
C учетом ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png) получаем ответ:
получаем ответ:
![(-\infty;-2]\cup \{2\}](/tpl/images/1361/5355/83f26.png)
3)
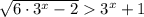
Так как 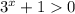 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
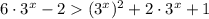
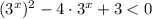
D=16-12=4
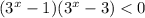
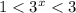
Показательная функция с основанием 3 возрастает
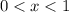
О т в е т. (0;1)
4)

Так как 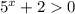 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
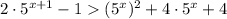
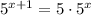
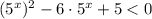
D=36-20=16
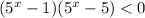
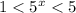
Показательная функция с основанием 5 возрастает
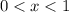
О т в е т. (0;1)
дана система:
2x+5y=1
x-10y=3
1. Выражаем
Видно что во втором уравнении имеется переменная X с коэффициентом 1,отсюда получается что легче всего выразить переменную Х из второго уравнения.
x=3+10y
2. После того как выразили подставляем в первое уравнение 3+10y вместо переменной Х.
2(3+10y)+5y=1
3. Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки )
6+20y+5y=1
25y=1-6
25y=-5
y=-5:25
y=-0,2
Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти Х и Y, потому что точка пересечения состоит их X и Y.Найдем X, в первом пункте где мы выражали туда подставляем Y.
x=3+10y
x=3+10*(-0,2)=1
Точки принято записывать на первом месте пишем переменную X, а на втором переменную Y.
ответ: (1; -0,2)