Ширина примерно равна 11м 53см, тогда длинна 17м 53см.
Площадь: 202кв. м
Объяснение:
Если мы возьмём ширину тренажёрного зала за "a", то длинна будет равна a+6.
Тогда ширина акробатического зала будет равна а+9, а ширина a+18(6+12).
Зная, что площадь акробатического зала равна 3 площади тренажёрного, то составляем уравнение:
3(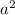
+6a)=(a+9)(a+18) - формула площади: S=x*y(где x - длинна, y - ширина)
Раскрываем скобки:
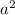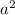3+18a=+9a+18a+162
Переносим в одну часть:
2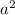-9а-162=0
Получили квадратичное уравнение, решаем методом дискриминанта:
D=b-4ac=81+1296=1377
D>0 => 2 корня уравнения.
x1,2=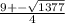
x1=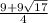
x2=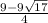
x1=-7.03 x2=11.53
Так как длинна не может быть отрицательна, ответ x2=a=11.53м
Подставляем а и найдём неизвестные величины.
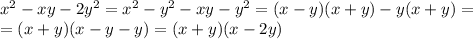
Мы разложили левую часть на два множителя. Число 7 — простое, поэтому оно может раскладываться ровно на две пары целых множителей: (1; 7) и (–1, –7). Тогда получим четыре системы:
Первая система:
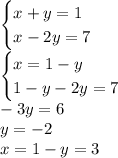
Вторая система:
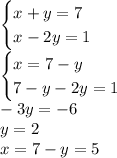
Третья система:
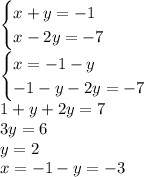
Четвёртая система:
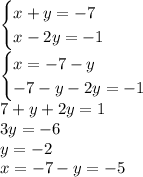
ответ: (3; –2), (–3; 2), (5; 2), (–5; –2).
P. S. Третью и четвёртую систему можно было бы не расписывать, если заметить, что при одновременной замене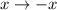 
и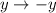 
значение выражения 
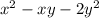не изменится. Это означает, что если (x; y) является решением, то (–x; –y) тоже является решением.
(x-3+2√2)(x-3-2√2)
Объяснение:
x²-6x+1
D=b²-4ac=36-4=32
√32= √4*4*2=4√2
x1=(-b-√d)2a=(6-4√2)/2=2(3-2√2)/2=3-2√2
x2=(-b+√d)2a=(6+4√2)/2=2(3+2√2)/2=3+2√2
ax²+bx+c=a(x–x1 )(x–x2)
x²-6x+1=1(x-(3-2√2))(x-(3+2√2))=(x-3+2√2)(x-3-2√2)