[-1; 1]
Объяснение:
(2·x-3)²≥ (3·x-2)²
(2·x-3)²-(3·x-2)²≥0
(2·x-3-3·x+2)·(2·x-3+3·x-2)≥0
(-x-1)·(5·x-5)≥0
(x+1)·(x-1)≤0
Рассмотрим уравнение:
(x+1)·(x-1)=0
x = -1, x = 1.
Ось Ох делится на промежутки (-∞; -1), (-1; 1) и (1; +∞) точками x = -1 и x = 1.
а) x∈(-∞; -1): (x+1)·(x-1)>0
б) x∈(-1; 1): (x+1)·(x-1)<0
в) x∈(1; +∞): (x+1)·(x-1)>0.
В силу равенства в неравенстве (x+1)·(x-1)≤0 ответом будет отрезок
[-1; 1].
(2x - 3)² ≥ (3x - 2)²,
4х² - 12х + 9 ≥ 9х² - 12х + 4,
4х² - 12х - 9х² + 12х ≥ 4 - 9,
-5х² ≥ -5,
х² ≤ 1,
|x| ≤ 1,
-1 ≤ x ≤ 1,
х ∈ [-1; 1].
ответ: [-1; 1].
1. а) 5xy³*(-2x²y)⁴ = 5xy³*16x⁸y⁴ = 80x¹⁺⁸y³⁺⁴ = 80x⁹y⁷
б) (2y-3x)² - (3x+2y)(2y-3x) = 4y²-12xy+9x²-6xy-9x²+4y²-6xy = 8y²-24xy
2. а) 4ab³-a³b = ab (4b²-a²) = ab (2b-a)(2b+a)
б) -9b-6b²-b³ = -b (9+6b+b²) = -b (b+3)²
3. 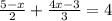
Здесь делаем всем НОЗ: 6.
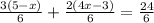
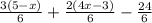
Теперь, когда у нас стали одинаковые знаменатели, решаем только числитель:
3(5-x)+2(4x-3)-24 = 0
15-3x+8x-6-24 = 0
-3x+8x+15-6-24 = 0
-5x-13 = 0
-5x = 13
x = -2,6
4. Увы, задачу не понял.
5. y = 4x-7 - линейная функция, графиком является прямая.
y = x+83 - линейная функция, графиком является прямая.
Построим таблицы:
1) y = 4x-7
x | 0 1
y | -7 -3
y₁ = 4*0-7 = -7
y₂ = 4*1-7 = -3
2) y = x+83
x | 0 1
y | 83 84
y₁ = 0+83 = 83
y₂ = 1+83 = 84
Как строить координатную плоскость - думаю, не надо объяснять.
ответ: у = -x^2+2(a-1)x+a^2. График - парабола, ветви которой вниз.
Раз два корня, то график пересекает ось Ох в двух точках, значит, вершина параболы должна быть в верхней полуплоскости. А раз число 1 находится между корнями,
то у (1) > 0
Имеем: y(1) = -1 + 2(а-1) + а^2
-1 + 2(а-1) + а^2 > 0
-1 + 2a - 2 + a^2 > 0
a^2 + 2a - 3 > 0
(a + 3)(a - 1) >0
a Є (- бесконечность; -3) U (1; +бесконечность)
2) D = (2 - m)^2 +4m + 12 = 4 - 4m + m^2 + 4m +12 =
= m^2 + 16 >0
(x1)^2 + (x2)^2 = (x1 + x2)^2 - 2x1x2
x1 + x2 = m - 2
x1x2 = -m - 3
(x1)^2 + (x2)^2 =(m - 2)^2 - 2(-m - 3) = m^2 - 4m + 4 + 2m + 6 =
= m^2 - 2m + 10.
Объяснение:
Минимальное значение будет при m = 2/2 = 1
x∈[-1;1]
Объяснение:
прощения, вот простое и правильное решение.