Уравнение касательной: 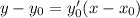
Отсюда: точка касания 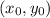 ;
;
точка пересечения с осью Ох 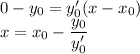
Расстояние от точки (0,0) до точки пересечения с осью Ох, конечно, равно 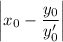
Расстояние от точки касания до точки пересечения с осью Ох:
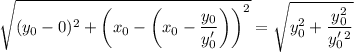
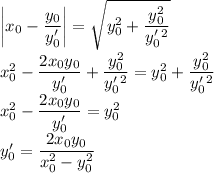
Перепишем в приличном виде:
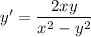
Положим y=xv, тогда y'=xv'+v:
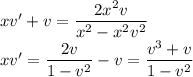
Это простейшее уравнение с разделяющимися переменными, решим его:
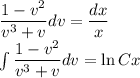
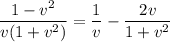
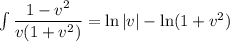
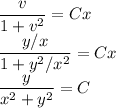
Это уравнение задает семейство окружностей с центром на оси ординат, проходящих через точку (0,0).
Учитывая, что окружность должна проходить через точку (2,2), находим значение С:
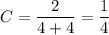
ответ. это окружность 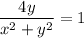 .
.
P.S. На самом деле, то, что должна получаться окружность, практически очевидно. Условие равенства отрезков касательной, проведенных из одной точки, известно еще из школьного курса геометрии.
P.P.S. На досуге можно подметить, что в точке (2,2) производная бесконечна, и в дифуре можно (?) найти некоторую неоднозначность...
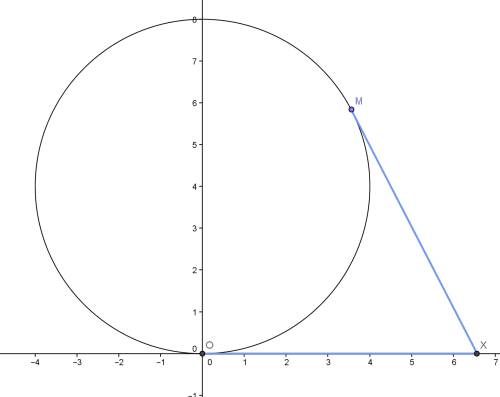
У треугольника вершины три. Значит, в любом случае, на одной из прямых будут лежать две вершины. Очевидно, что тогда все треугольники разделятся на два класса, те у которых две вершины на первой прямой, и те, у которых - на второй. Выбрать две точки из 12 можно числом сочетаний. На каждые такие точки приходится 13 возможных третьих вершин.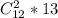 . (Аналогично для другой прямой)
. (Аналогично для другой прямой)  - треугольников.
- треугольников.
Четырехугольник имеет четыре вершины, потому имеет смысл рассматривать один их класс (ведь на каждой прямой может быть только две вершины (ибо у четырехугольника три вершины не могут лежать на одной прямой)) Выбрать первые две можно так: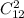 , каждой такой паре соответствует
, каждой такой паре соответствует 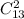 пар вершин на второй стороне. тогда прямоугольников
пар вершин на второй стороне. тогда прямоугольников 