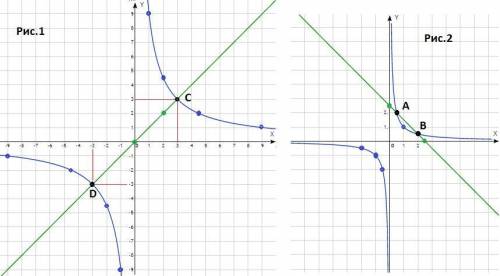
1. Обратно пропорциональная зависимость :
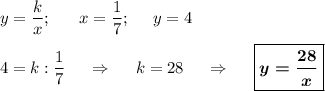
2. Решите графически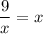 
График функции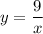 
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение 
График функции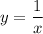 
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами.
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить а В то выполнить одно любое из этих действий (либо А, либо В) можно
Качественная расстановка спортсменов на игровых позициях приносит максимальную результативность матчей, за счет полного раскрытия достоинств.
Всего существует 11 футбольных амплуа, 10 из которых считаются полевыми игроками и вратарь.
ответ: функция имеет разрыв первого рода в точке x=-1 и непрерывна при других значениях x.
Объяснение:
Зададим функцию в виде:
f(x)=1, если -∞<x<-1;
f(x)=x, если -1≤x≤1;
f(x)=1, если 1<x<∞.
1. Отсюда следует, что если x⇒-1 "слева", то есть оставаясь меньшим, чем -1, то lim (fx)=lim 1=1. Если же x⇒-1 "справа", то есть оставаясь большим, чем -1, то lim f(x)=lim(x)=-1. Таким образом, в точке x=-1 функция имеет конечные и при этом разные пределы "слева" и "справа" - а это значит, что в этой точке она терпит разрыв 1-го рода.
2. Рассмотрим теперь точку x=1. Если x⇒1 "слева", то lim (fx)=lim x=1. Если x⇒1 "справа", то lim f(x)=lim 1=1. Таким образом, в точке x=1 функция имеет конечные и при этом равные пределы "слева" и "справа" - а это означает, что в этой точке она не имеет разрыва, т.е непрерывна.