Question

Вычислите производную в точке x0

Answer 1

$f(x)=x^2;\: \Delta y=f(x_0+\Delta x)-f(x_0); \: \Delta y=(x_0+\Delta x)^2-x_0^2; \\ \Delta y = x^2_0 +2\cdot x_0 \cdot \Delta x+(\Delta x)^2-x^2_0=2\cdot x_0 \cdot \Delta x + (\Delta x)^2; \; \\ \boxed{\Delta y =2\cdot x_0 \cdot \Delta x + (\Delta x)^2}$

Теперь вспоминаем определение производной в точке

$$y(x_0)' = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} =\lim_{\Delta x \to 0} \frac{2\cdot x_0 \cdot \Delta x +(\Delta x)^2}{\Delta x} =$

$$=\lim_{\Delta x \to 0} \frac{\Delta x}{\Delta x} \bigg(2\cdot x_0 + \Delta x \bigg) = \lim_{\Delta x \to 0} (2\cdot x_0+\Delta x)=2 x_0$

Итак, производная равна:

$\boxed{y'(x_0)=2x_0} \;(y=x^2)$

Или, если принять во внимание, что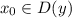 $x_0 \in D(y)$

То есть это правило выполняется для любого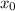 $x_0$ из области определения функции, следовательно,

$\boxed{(x^2)'= 2x}$