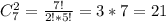 , всего выбрать два черных шара:
, всего выбрать два черных шара: 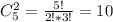 . Вероятность:
. Вероятность: 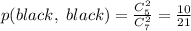
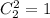
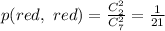
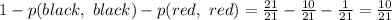
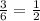 . На второй подойдут 3, 4, 5, 6. Вероятность выпадения
. На второй подойдут 3, 4, 5, 6. Вероятность выпадения 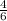 . Т.к. события независимые, то вероятности перемножаем.
. Т.к. события независимые, то вероятности перемножаем. 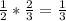 .
.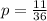
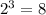 вариантов: ннн, ппп, нпп, ннп, пнп, ппн, пнн, пнп.
вариантов: ннн, ппп, нпп, ннп, пнп, ппн, пнн, пнп.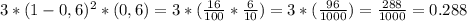
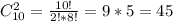
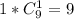 .
.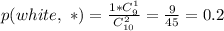
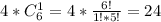 (т.к. не чёрных у нас 6, 5 красных и 1 белый.)
(т.к. не чёрных у нас 6, 5 красных и 1 белый.)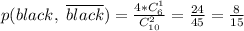
1.(n + 29)(n + 3) - (n + 7)(n + 1) = n² + 3n + 29n + 87 - n² - n - 7n - 7 (раскрыли скобки)
2. 24n + 80(привели подобные)
3. 8(3n+10) - вынесли 8 за скобки ⇒один из множителей делится на 8 ⇒ значение данного выражения при всех натуральных значениях n делится на 8.