5,25
Объяснение:
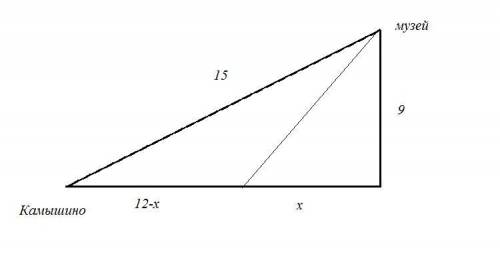
Вся система представляет собой прямоугольный треугольник, где один катет - это расстояние по реке, другой расстояние от реки до поселка 9 км, и гипотенузой 15 км.
Найдем расстояние по реке:
√(15²-9²)=√144=12 км
Пусть расстояние, которое они могли бы проплыть езе по реке х км, тогда на байдарках туристы проплыли (12-х) км. А время затраченное на путь: (12-х)/5 ч.
По лесу тогда осталось пройти расстояние: √(9²+х²) км, при этом затраченное время по лесу: √(81+х²) ч.
Общее время:
(12-х)/5+√(81+х²)/3
Чтобы найти точку минимума, найдем производную.
((12-х)/5+√(81+х²)/3)'=-1/5+(81+x²)'*1/2/(3√(x²+81))=-1/5+x/(3√(x²+81))
Приравняем производную к 0.
-1/5+x/(3√(x²+81))=0
x/(3√(x²+81))=1/5
5х=3√(x²+81)
25х²=9(х²+81)
25х²-9х²=729
16х²=729
х=±6,75
- - +
_________-6,75___________6,75________
Значит точка минимума функции 6,75.
Найдем раcстояние от Кмышино, на котором туристы оставили байдарки.
12-6,75=5,25 км
b∈(-∞; -8)∪(8; +∞)
Объяснение:
Квадратное уравнение вида a·x²+b·x+c=0 имеет два различных корня, если
D= b² - 4·a·c>0.
Дано квадратное уравнение 2·x²-b·x+8=0, где b - параметр. Это квадратное уравнение имеет два различных корня, если
D = (-b)² - 4·2·8>0.
Решаем последнее неравенство:
(-b)² - 4·2·8>0
b² - 8² >0
(b+8)·(b-8)>0
Применим метод интервалов и определим знак выражения:
(b+8)·(b-8) + - +
(-8)0(8)>x
Тогда: b∈(-∞; -8)∪(8; +∞)
решение задания смотри на фотографии