Нужна !
решить систему линейных уравнений методом крамера:

👇

Ответ:

halilappazov

22.05.2021

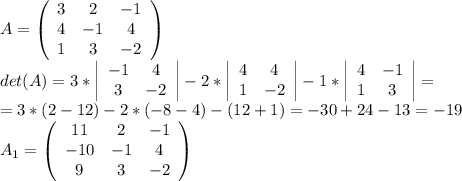
$A=\left(\begin{array}{ccc}3&2&-1\\4&-1&4\\1&3&-2\end{array}\right)\\det(A)=3*\left|\begin{array}{cc}-1&4\\3&-2\end{array}\right|-2*\left|\begin{array}{cc}4&4\\1&-2\end{array}\right|-1*\left|\begin{array}{cc}4&-1\\1&3\end{array}\right|=\\=3*(2-12)-2*(-8-4)-(12+1)=-30+24-13=-19\\A_1=\left(\begin{array}{ccc}11&2&-1\\-10&-1&4\\9&3&-2\end{array}\right)\\$

$det(A_1)=11*\left|\begin{array}{cc}-1&4\\3&-2\end{array}\right|-2*\left|\begin{array}{cc}-10&4\\9&-2\end{array}\right|-1*\left|\begin{array}{cc}-10&-1\\9&3\end{array}\right|=\\=11*(2-12)-2(20-36)-(-30+9)=-110+32+21=-57$

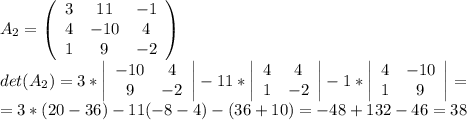
$A_2=\left(\begin{array}{ccc}3&11&-1\\4&-10&4\\1&9&-2\end{array}\right)\\det(A_2)=3*\left|\begin{array}{cc}-10&4\\9&-2\end{array}\right|-11*\left|\begin{array}{cc}4&4\\1&-2\end{array}\right|-1*\left|\begin{array}{cc}4&-10\\1&9\end{array}\right|=\\=3*(20-36)-11(-8-4)-(36+10)=-48+132-46=38$

$A_3=\left(\begin{array}{ccc}3&2&11\\4&-1&-10\\1&3&9\end{array}\right)\\det(A_3)=3*\left|\begin{array}{cc}-1&-10\\3&9\end{array}\right|-2*\left|\begin{array}{cc}4&-10\\1&9\end{array}\right|+11*\left|\begin{array}{cc}4&-1\\1&3\end{array}\right|=\\=3(-9+30)-2(36+10)+11(12+1)=63-92+143=114$

$x_1=\frac{det(A_1)}{det(A)}=\frac{-57}{-19}=3$

$x_2=\frac{det(A_2)}{det(A)}=\frac{38}{-19}=-2 \\x_3=\frac{det(A_3)}{det(A)} =\frac{114}{-19} =-6$

4,4(66 оценок)

Ответ:

гульназ85

22.05.2021

x1 x2 x3 B

3 2 -1 | 3 2 11

4 -1 4 | 4 -1 -10

1 3 -2 | 1 3 9

Определитель находим по треугольной схеме.

Д = 3*-1*-2 + 2*4*1 + -1*4*3 - 2*4*-2 - 3*4*3 - -1*-1*1 = 6 + 8 - 12 + 16 - 36 -1 = -19.

Заменяем 1-й столбец на вектор результатов B:

11 2 -1 | 11 2

-10 -1 4 | -10 -1

9 3 -2 | 9 3 =

= 22 + 72 + 30 - 40 - 132 - 9 = -57.

Определитель Д1 равен -57.

Заменяем 2-й столбец на вектор результатов B:

3 11 -1 | 3 11

4 -10 4 | 4 -10

1 9 -2 | 1 9 =

= 60 + 44 - 36 + 88 - 108 - 10 = 38.

Определитель Д2 равен 38.

Заменяем 3-й столбец на вектор результатов B:

3 2 11 | 3 2

4 -1 -10 | 4 -1

1 3 9 | 1 3 =

= -27 - 20 + 132 - 72 + 90 + 11 = 114.

Определитель Д3 равен 114.

x1 = Д1/Д = -57 /-19 = 3

x2 = Д2/Д= 38 /-19 = -2

x3 = Д3/Д= 114 /-19 = -6.

4,8(21 оценок)

Открыть все ответы

Ответ:

funnybotan2000

22.05.2021

Объяснение:

б) можно загнать под общий корень

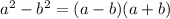твой пример $=\sqrt[7]{(5-\sqrt{26})(5+\sqrt{26}) }=$ по формуле сокращенного умножения a^2-b^2=(a-b)(a+b) = $\sqrt[7]{5^2-\sqrt{26}^2} =\sqrt[7]{25-26} =\sqrt[7]{-1} =$ так как корень нечетный можно выводить из под корня отрицательное число =

= $\sqrt[7]{-1} =-1$

в) по правилу $\sqrt[a]{b^n}=b^{\frac{n}{a} }$

$\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *\sqrt[3]{2}=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *2^{\frac{1}{3} }=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *2^{\frac{2}{6} }=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *\sqrt[6]{4}$

коротко если говорить я сделал знаменатель равным 6-ти, чтобы объединить корни

$\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2} *\sqrt[6]{4}=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{2*4}=\sqrt[3]{-2\sqrt{2} }+\sqrt[6]{8}$

вынесем минус

$-\sqrt[3]{2\sqrt{2} }+\sqrt[6]{8}= -\sqrt[3]{2\sqrt{2} }+\sqrt[3]{2\sqrt{2} }=0$

почему?

$\sqrt[6]{8}=\sqrt[6]{2*4}=\sqrt[6]{2*2^2}=\sqrt[6]{\sqrt{2}^2*2^2 } =\sqrt{2}^{\frac{2}{6} }*2^{\frac{2}{6} }= \sqrt{2}^{\frac{1}{3} }*2^{\frac{1}{3} }=\sqrt[3]{2\sqrt{2} }$

$-a+a=0\\a=\sqrt[n]{2\sqrt{3} }$

еще 2 примера

ну ладно

$\sqrt[4]{7+4\sqrt{3} } *\sqrt{2-\sqrt{3} }$

чтобы сделать под общий корень, нужно чтобы степень корней была одинакова

$=\sqrt[4]{(7+4\sqrt{3})((2-\sqrt{3})^2) } =$

формула сокращенного умножения

$\sqrt[4]{(7+4\sqrt{3})(4-4\sqrt{3}+3) }=\sqrt[4]{(7+4\sqrt{3})(7-4\sqrt{3})} =\sqrt[4]{49-48} =\sqrt[4]{1} =1$

тут всё знакомо с предыдущих

ну кроме того что $\sqrt{x} =\sqrt[2]{x}$ = $\sqrt[4]{x^2}$ = $x^{\frac{2}{4} }=x^{\frac{1}{2} }$

d) $\sqrt{3+\sqrt[4]{(-8)^2}} -\sqrt{3-\sqrt[4]{(-8)^2}}=\sqrt{3+\sqrt[4]{64}}-\sqrt{3-\sqrt[4]{64}}=\sqrt{3+\sqrt[4]{2^6}}-\sqrt{3-\sqrt[4]{2^6}}=\sqrt{3+2\sqrt{2} }-\sqrt{3-2\sqrt{2} }$