знаменатель геометрической прогрессии - это q
система уравнений:
b1=4, b1=4, b1=4, b1=4,
b3=108 b1*q²=108 4*q²=108 q²=27
значит q= ± √27=±3√3
√-это корень
но по характеристическому свойству геом. прогр.
b2-это положительное число, то
только q=3√3 удовлетворяет условию
ответ:q=3√3
41-32х≥0;
9-3х≥0
5+х≥0
ОДЗ: х ∈[-5; 41/32]
Перепишем уравнение в виде
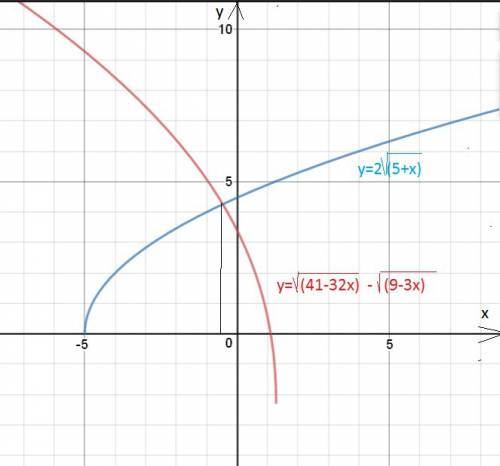
√(41-32x)=2√(5+x)+√(9-3x)
Возводим в квадрат.
41-32х=4(5+х)+4√(5+х)·√(9-3х)+9-3х
4√(5+х)·√(9-3х)=12-33х
Возводим в квадрат при условии 12-33х≥0 ⇒ х ≤12/33.
16(5+х)(9-3х)=144-792х+1089х²;
1137х²-696х-576=0
379х²-232х-192=0
D=(-232)²-4·379·(-192)=53 824+291 072=344 896
x=(232-√344896)/758≈-0,47 или х=(232+√344896)/758≈1,08 - не удовлетворяет условию х ≤12/33, поэтому не является корнем уравнения
bn = b1 * q^n-1
b3 = 4 * q^2
108 = 4*q^2
27 = q^2
q = 3 корня из 3 (3*sqrt(3))